题目内容
已知函数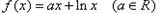
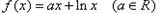
(1)若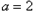 ,求曲线
,求曲线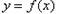 在
在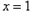 处切线的斜率;
处切线的斜率;
(2)当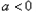 时,求
时,求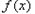 的单调区间;
的单调区间;
(3)设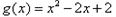 ,若对任意
,若对任意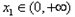 ,均存在
,均存在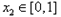 ,使得
,使得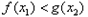 ,求
,求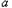 的取值范围.
的取值范围.
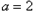 ,求曲线
,求曲线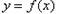 在
在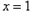 处切线的斜率;
处切线的斜率;(2)当
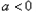 时,求
时,求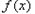 的单调区间;
的单调区间;(3)设
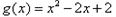 ,若对任意
,若对任意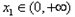 ,均存在
,均存在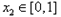 ,使得
,使得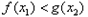 ,求
,求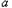 的取值范围.
的取值范围.解:(Ⅰ)由已知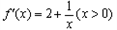 ,
,
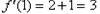 .
.
故曲线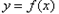 在
在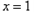 处切线的斜率为
处切线的斜率为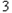 .
.
(Ⅱ)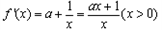 .
.
当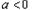 时,由
时,由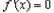 ,得
,得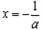 .在区间
.在区间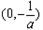 上,
上,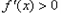 ;
;
在区间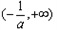 上,
上,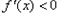 ,
,
所以,函数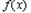 的单调递增区间为
的单调递增区间为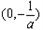 ,单调递减区间为
,单调递减区间为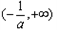
(Ⅲ)由已知转化为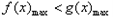 .
. 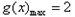
由(Ⅱ)知,当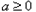 时,
时,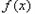 在
在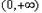 上单调递增,值域为
上单调递增,值域为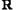 ,故不符合题意
,故不符合题意
.(或者举出反例:存在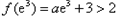 ,故不符合题意.)
,故不符合题意.)
当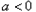 时,
时,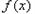 在
在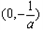 上单调递增,在
上单调递增,在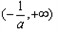 上单调递减,
上单调递减,
故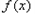 的极大值即为最大值,
的极大值即为最大值,
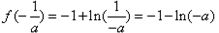 ,
,
所以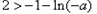 ,解得
,解得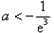 .
.
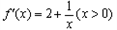 ,
, 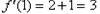 .
.故曲线
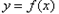 在
在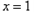 处切线的斜率为
处切线的斜率为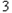 .
. (Ⅱ)
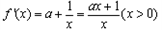 .
. 当
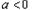 时,由
时,由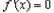 ,得
,得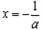 .在区间
.在区间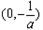 上,
上,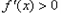 ;
;在区间
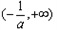 上,
上,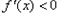 ,
,所以,函数
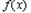 的单调递增区间为
的单调递增区间为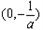 ,单调递减区间为
,单调递减区间为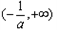
(Ⅲ)由已知转化为
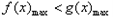 .
. 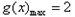
由(Ⅱ)知,当
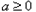 时,
时,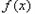 在
在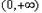 上单调递增,值域为
上单调递增,值域为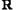 ,故不符合题意
,故不符合题意.(或者举出反例:存在
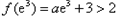 ,故不符合题意.)
,故不符合题意.) 当
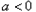 时,
时,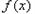 在
在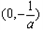 上单调递增,在
上单调递增,在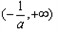 上单调递减,
上单调递减,故
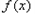 的极大值即为最大值,
的极大值即为最大值,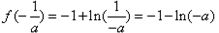 ,
, 所以
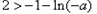 ,解得
,解得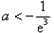 .
. 
练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

 的表达式;
的表达式; 上是单调函数.
上是单调函数.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数
 ,求
,求 的零点;
的零点; 上有两个不同的零点,求
上有两个不同的零点,求 的取值范围。
的取值范围。