题目内容
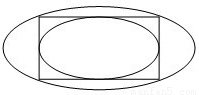
 把离心率相同的椭圆叫做“相似椭圆”,如图的两个相似椭圆,分别是同一个矩形的内切椭圆和外接椭圆,且q(q>1)是这两个椭圆长轴的长的比值,那么q=
把离心率相同的椭圆叫做“相似椭圆”,如图的两个相似椭圆,分别是同一个矩形的内切椭圆和外接椭圆,且q(q>1)是这两个椭圆长轴的长的比值,那么q=| 2 |
| 2 |
分析:设外椭圆的方程为
+
=1(m>n>0),内椭圆的方程为
+
=1(a>b>0),利用e=
=
结合合比定理即可求得q.
| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| c1 |
| m |
| c2 |
| a |
解答:解:设外椭圆的方程为
+
=1(m>n>0),c1为其半焦距,
内椭圆的方程为
+
=1(a>b>0),c2,
∵两椭圆的离心率相等,
∴e=
=
,
∴
=
,
∴(
)2=(
)2=
=
,
∴
=
=
,①
依题意P(a,b)为外椭圆为
+
=1上的点,
∴
+
=1②
由①②得:2
=1,
∴
=
,
=2,
∴
=
.即q=
=
=
.
故答案为:
.
| x2 |
| m2 |
| y2 |
| n2 |
内椭圆的方程为
| x2 |
| a2 |
| y2 |
| b2 |
∵两椭圆的离心率相等,
∴e=
| c1 |
| m |
| c2 |
| a |
∴
| m |
| a |
| c1 |
| c2 |
∴(
| m |
| a |
| c1 |
| c2 |
| m2-c12 |
| a2-c22 |
| n2 |
| b2 |
∴
| m |
| a |
| c1 |
| c2 |
| n |
| b |
依题意P(a,b)为外椭圆为
| x2 |
| m2 |
| y2 |
| n2 |
∴
| a2 |
| m2 |
| b2 |
| n2 |
由①②得:2
| a2 |
| m2 |
∴
| a2 |
| m2 |
| 1 |
| 2 |
| m2 |
| a2 |
∴
| m |
| a |
| 2 |
| 2m |
| 2a |
| m |
| a |
| 2 |
故答案为:
| 2 |
点评:本题考查椭圆的简单性质,考查转化思想与运算能力,考查合分比定理,属于难题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
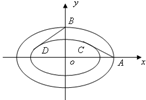 简化的北京奥运会主体育场“鸟巢”的钢结构俯视图如图所示,内外两圈的钢骨架是离心率相同的椭圆,外层椭圆顶点向内层椭圆引切线AC,BD,设内层椭圆方程为
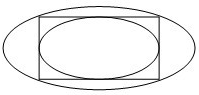
简化的北京奥运会主体育场“鸟巢”的钢结构俯视图如图所示,内外两圈的钢骨架是离心率相同的椭圆,外层椭圆顶点向内层椭圆引切线AC,BD,设内层椭圆方程为 把离心率相同的椭圆叫做“相似椭圆”,如图的两个相似椭圆,分别是同一个矩形的内切椭圆和外接椭圆,且q(q>1)是这两个椭圆长轴的长的比值,那么q=________.
把离心率相同的椭圆叫做“相似椭圆”,如图的两个相似椭圆,分别是同一个矩形的内切椭圆和外接椭圆,且q(q>1)是这两个椭圆长轴的长的比值,那么q=________.