Question

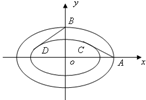简化的北京奥运会主体育场“鸟巢”的钢结构俯视图如图所示，内外两圈的钢骨架是离心率相同的椭圆，外层椭圆顶点向内层椭圆引切线AC，BD，设内层椭圆方程为

x2

a2

+

y2

b2

=1(a＞b＞0)，则外层椭圆方程可设为

x2

(ma)2

+

y2

(mb)2

=1(a＞b＞0，m＞1)．若AC与BD的斜率之积为-

9

16

，则椭圆的离心率为（　　）

• A、

  7

  4

• B、

  2

  2

• C、

  6

  4

• D、

  3

  4

Answer 1

分析：设出切线AC和BD的方程，与椭圆方程联立消去y，根据判别式等于0求得k₁和k₂的表达式，根据AC与BD的斜率之积求得a和b的关系，进而求得a和c的关系，椭圆的离心率可得．

解答：解：设切线AC的方程为y=k₁（x-ma），则

y=k 1(x-ma) (bx)2+(ay) 2=(ab) 2

消去y得（b²+a²k₁²）x²-2ma³k₁²x+m²a⁴k₁²-a²b²=0
由△=0?k₁²=

b2

a2

•

1

m2-1

，同理k₂²=

b2

a2

•（m²-1）
∴k₁²•k₂²=

b4

a4

∴

b2

a2

=

9

16

，
∴e=

7

4

，
故选A．

点评：本题主要考查了椭圆的简单性质和直线与椭圆的位置关系，考查了学生综合分析问题和解决问题的能力，解题过程要注意运算的正确性．