题目内容
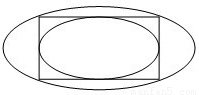
 把离心率相同的椭圆叫做“相似椭圆”,如图的两个相似椭圆,分别是同一个矩形的内切椭圆和外接椭圆,且q(q>1)是这两个椭圆长轴的长的比值,那么q=________.
把离心率相同的椭圆叫做“相似椭圆”,如图的两个相似椭圆,分别是同一个矩形的内切椭圆和外接椭圆,且q(q>1)是这两个椭圆长轴的长的比值,那么q=________.

分析:设外椭圆的方程为
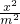 +
+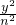 =1(m>n>0),内椭圆的方程为
=1(m>n>0),内椭圆的方程为 +
+ =1(a>b>0),利用e=
=1(a>b>0),利用e= =
= 结合合比定理即可求得q.
结合合比定理即可求得q.解答:设外椭圆的方程为
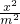 +
+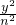 =1(m>n>0),c1为其半焦距,
=1(m>n>0),c1为其半焦距,内椭圆的方程为
 +
+ =1(a>b>0),c2,
=1(a>b>0),c2,∵两椭圆的离心率相等,
∴e=
 =
= ,
,∴
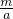 =
= ,
,∴
 =
= =
= =
=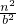 ,
,∴
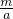 =
= =
= ,①
,①依题意P(a,b)为外椭圆为
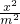 +
+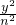 =1上的点,
=1上的点,∴
 +
+ =1②
=1②由①②得:2
 =1,
=1,∴
 =
= ,
,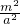 =2,
=2,∴
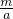 =
= .即q=
.即q= =
=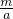 =
= .
.故答案为:
 .
.点评:本题考查椭圆的简单性质,考查转化思想与运算能力,考查合分比定理,属于难题.

练习册系列答案
相关题目
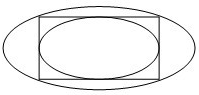 把离心率相同的椭圆叫做“相似椭圆”,如图的两个相似椭圆,分别是同一个矩形的内切椭圆和外接椭圆,且q(q>1)是这两个椭圆长轴的长的比值,那么q=
把离心率相同的椭圆叫做“相似椭圆”,如图的两个相似椭圆,分别是同一个矩形的内切椭圆和外接椭圆,且q(q>1)是这两个椭圆长轴的长的比值,那么q=