题目内容
如图，n2（n≥4）个正数排成n行n列方阵：符号aij（1≤i，j≤n）表示位于第i行第j列的正数．已知每一行的数成等差数列，每一列的数成等比数列，且各列数的公比都等于q．若
，a24=1，
，则q= ，aij= ．
【答案】分析：设第一行的公差为d，进而根据a24=1，
，利用等差数列和等比数列的通项公式可得方程组求得q和d，进而求得aij．
解答：解：设第一行的公差为d，依题意可知
，解得q=
，d=
∴aij=[
+（j-1）
]（
）i-1=
故答案为
，
点评：本题主要考查了等差数列和等比数列的通项公式．本题主要考查了学生对等差数列和等比数列的理解和灵活运用．
，利用等差数列和等比数列的通项公式可得方程组求得q和d，进而求得aij．解答：解：设第一行的公差为d，依题意可知
，解得q=，d=∴aij=[
+（j-1）]（）i-1=故答案为
，点评：本题主要考查了等差数列和等比数列的通项公式．本题主要考查了学生对等差数列和等比数列的理解和灵活运用．
练习册系列答案
相关题目
如图，n2（n≥4）个正数排成n行n列方阵：符号aij（1≤i，j≤n）表示位于第i行第j列的正数．已知每一行的数成等差数列，每一列的数成等比数列，且各列数的公比都等于q．若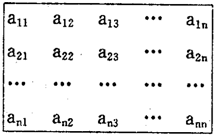
（2012•洛阳一模）如图，n2（n≥4）个正数排成n×n方阵，aij（1≤i，j≤n）表示位于第i行第j列的正数．已知每一行的数成等差数列，每一列的数成等比数列，且每一列数的公比都等于q．若a11=1，a23=1，a32=
．