题目内容
如图,n2(n≥4)个正数排成n行n列方阵,其中每一行的数成等差数列,每一列的数成等比数列,并且所有公比都相等,设 .
.(1)求公比q的值;
(2)求a1k(1≤k≤n)的值;
(3)求Sn=a11+a22+a33+…+ann的值.
【答案】分析:(1)通过数列每一行的数成等差数列,求出a44,每一列的数成等比数列,即可求公比q的值;
(2)求出数列的公差,利用通项公式直接求解a1k(1≤k≤n)的值;
(3)利用塑料袋通项公式,通过错位相减法直接求解Sn=a11+a22+a33+…+ann的值.
解答:解:(1)因为每一行的数成等差数列, ,∴
,∴ ,
,
每一列的数成等比数列a24=1 ,
,
因为正数排成n行n列方阵,
所以q>0,
解得q= .
.
(2)∵a ∴a12=1
∴a12=1
∵ ∴
∴
∵{a1k}成等差数列 ,
,

(3)∵
Sn=a11+a22+a33+…+ann
∴ ,
,
则 ,
,
∴ ,
,
∴
点评:本题考查等差数列与等比数列的关综合应用,考查数列求和的常用方法,考查分析问题解决问题的能力.
(2)求出数列的公差,利用通项公式直接求解a1k(1≤k≤n)的值;
(3)利用塑料袋通项公式,通过错位相减法直接求解Sn=a11+a22+a33+…+ann的值.
解答:解:(1)因为每一行的数成等差数列,
 ,∴
,∴ ,
,每一列的数成等比数列a24=1
 ,
,因为正数排成n行n列方阵,
所以q>0,
解得q=
 .
.(2)∵a
 ∴a12=1
∴a12=1∵
 ∴
∴
∵{a1k}成等差数列
 ,
,
(3)∵

Sn=a11+a22+a33+…+ann
∴
 ,
,则
 ,
,
∴
 ,
,∴

点评:本题考查等差数列与等比数列的关综合应用,考查数列求和的常用方法,考查分析问题解决问题的能力.

练习册系列答案
相关题目
 如图,n2(n≥4)个正数排成n行n列方阵:符号aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都等于q.若
如图,n2(n≥4)个正数排成n行n列方阵:符号aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都等于q.若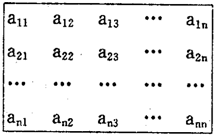 (2012•洛阳一模)如图,n2(n≥4)个正数排成n×n方阵,aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且每一列数的公比都等于q.若a11=1,a23=1,a32=
(2012•洛阳一模)如图,n2(n≥4)个正数排成n×n方阵,aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且每一列数的公比都等于q.若a11=1,a23=1,a32= 如图,n2(n≥4)个正数排成n行n列方阵:符号aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都等于q.若
如图,n2(n≥4)个正数排成n行n列方阵:符号aij(1≤i,j≤n)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都等于q.若 ,a24=1,
,a24=1, ,则q= ,aij= .
,则q= ,aij= .