题目内容
双曲线C：
(a＞0，b＞0)的离心率为2，且
，其中A(0，-b)，B(a，0).(Ⅰ)求双曲线C的方程；
(Ⅱ)若双曲线C上存在关于直线l:y=kx+4对称的点，求实数k的取值范围.
解:（Ⅰ）依题意有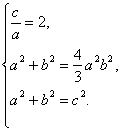
解得：a=1,b=,c=2.
所求双曲线的方程为x2-
（Ⅱ）当k=0时，显然不存在.
当k≠0时，设双曲线上两点M、N关于直线l对称，由l⊥MN,直线MN的方程为y=-
x+m,则M、N两点的坐标满足方程组
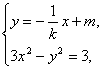消去y得(3k2-1)x2+2kmx-(m2+3)k2=0.
显然3k2-1≠0,
∴Δ=(2km)2-4(3k2-1)[-(m2+3)k2]＞0.
即k2m2+3k2-1＞0. ①
设线段MN中点D（x0,y0）.
则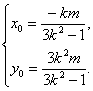
∵D(x0,y0)在直线l上，
∴
即k2m=3k2-1 ②
把②代入①中得 k2m2+mk2＞0,
解得m＞0或m＜-1.
∴
＞0或
＜-1.
则|k|＞
或|k|＜
,且k≠0.
∴k的取值范围是
(-∞,-
)∪(
,0)∪(0,
)∪(
,+∞).
练习册系列答案
相关题目
(a＞0，b＞0)的左、右焦点，过F1的直线
与
的左、右两支分别交于A，B两点．若|AB|:|BF2|:|AF2|＝3:4:5，则双曲线的离心率为（
）
B．
C．2
D．
(a＞0，b＞0)的左、右焦点，过F1的直线
与
的左、右两支分别交于A，B两点．若
ABF2为等边三角形，则双曲线的离心率为（ ）
B．2
C． 
D．
(a>0,b>0)的两个焦点。若在C上存在一点P。使PF1⊥PF2，且∠PF1F2=30°，则C的离心率为________________.
(a＞0，b＞0)的左、右焦点，过F1的直线
与
的左、右两支分别交于A，B两点．若 | AB | : | BF2
| : | AF2 |＝3:4 : 5，则双曲线的离心率为
B．
C．2 D．
(a＞0，b＞0)的右焦点为F，左、右顶点分别为A1、A2．过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P，若P恰好在以A1A2为直径的圆上，则双曲线C的离心率为 (
)
B． 2 C． 
D． 3