题目内容
如图,F1,F2是双曲线C: (a>0,b>0)的左、右焦点,过F1的直线
(a>0,b>0)的左、右焦点,过F1的直线 与
与 的左、右两支分别交于A,B两点.若 | AB | : | BF2
| : | AF2 |=3:4 : 5,则双曲线的离心率为
的左、右两支分别交于A,B两点.若 | AB | : | BF2
| : | AF2 |=3:4 : 5,则双曲线的离心率为

A. B.
B. C.2 D.
C.2 D.
【答案】
A
【解析】
试题分析:∵|AB|:|BF2|:|AF2|=3:4:5,不妨令|AB|=3,|BF2|=4,|AF2|=5,
∵|AB|2+|BF2|2=|AF2|2,
∴∠ABF2=90°,
又由双曲线的定义得:|BF1|-|BF2|=2a,|AF2|-|AF1|=2a,
∴|AF1|+3-4=5-|AF1|,
∴|AF1|=3.
∴|BF1|-|BF2|=3+3-4=2a,
∴a=1.
在Rt△BF1F2中,|F1F2|2=|BF1|2+|BF2|2=62+42=52,又|F1F2|2=4c2,
∴4c2=52,∴c= .
.
∴双曲线的离心率e=
考点:双曲线的简单性质
点评:本题考查双曲线的简单性质,求得a与c的值是关键,考查转化思想与运算能力,属于中档题.

练习册系列答案
相关题目
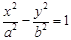 (a>0,b>0) 的左、右焦点,过F1的直线与
(a>0,b>0) 的左、右焦点,过F1的直线与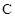 的左、右两支分别交于A,B两点.若 | AB | : | BF2
| : | AF2 |=3 : 4
: 5,则双 曲线的离心率为 .
的左、右两支分别交于A,B两点.若 | AB | : | BF2
| : | AF2 |=3 : 4
: 5,则双 曲线的离心率为 .