题目内容
已知椭圆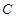 :
: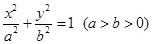 的左、右焦点分别为
的左、右焦点分别为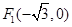 、
、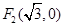 ,椭圆上的点
,椭圆上的点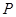 满足
满足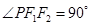 ,且△
,且△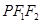 的面积为
的面积为 .
.
(Ⅰ)求椭圆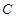 的方程;
的方程;
(Ⅱ)设椭圆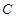 的左、右顶点分别为
的左、右顶点分别为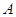 、
、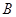 ,过点
,过点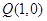 的动直线
的动直线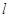 与椭圆
与椭圆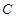 相交于
相交于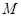 、
、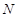 两点,直线
两点,直线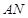 与直线
与直线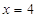 的交点为
的交点为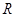 ,证明:点
,证明:点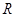 总在直线
总在直线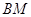 上.
上.
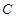 :
: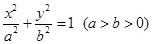 的左、右焦点分别为
的左、右焦点分别为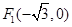 、
、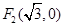 ,椭圆上的点
,椭圆上的点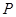 满足
满足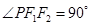 ,且△
,且△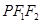 的面积为
的面积为 .
.(Ⅰ)求椭圆
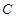 的方程;
的方程;(Ⅱ)设椭圆
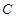 的左、右顶点分别为
的左、右顶点分别为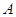 、
、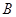 ,过点
,过点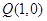 的动直线
的动直线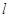 与椭圆
与椭圆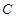 相交于
相交于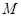 、
、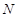 两点,直线
两点,直线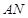 与直线
与直线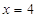 的交点为
的交点为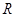 ,证明:点
,证明:点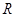 总在直线
总在直线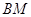 上.
上.(Ⅰ)椭圆 的方程为
的方程为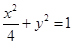 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
 的方程为
的方程为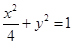 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.试题分析:(Ⅰ)由焦点坐标知:
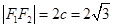 .又椭圆上的点
.又椭圆上的点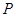 满足
满足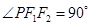 ,由
,由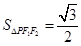 可求得
可求得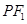 ,再由勾股定理可求得
,再由勾股定理可求得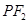 ,从而求得
,从而求得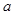 .再由
.再由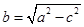 求得
求得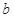 ,从而得椭圆的方程.(Ⅱ)首先考虑
,从而得椭圆的方程.(Ⅱ)首先考虑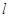 与
与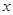 轴垂直的情况,此时可求出直线
轴垂直的情况,此时可求出直线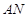 与直线
与直线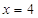 的交点为
的交点为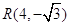 ,
,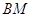 的方程是:
的方程是: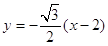 ,代入验证知点
,代入验证知点 在直线
在直线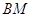 上.当直线
上.当直线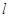 不与
不与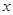 轴垂直时,设直线
轴垂直时,设直线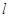 的方程为
的方程为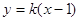 ,点
,点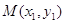 、
、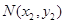 ,
,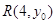 ,则
,则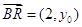 ,
,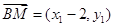 ,要证明
,要证明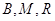 共线,只需证明
共线,只需证明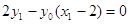 ,即证明
,即证明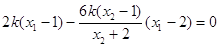 .
.若
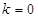 ,显然成立;若
,显然成立;若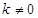 , 即证明
, 即证明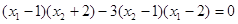
而
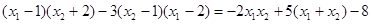 ,这显然用韦达定理.
,这显然用韦达定理.试题解析:(Ⅰ)由题意知:
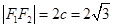 , 1分
, 1分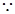 椭圆上的点
椭圆上的点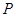 满足
满足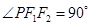 ,且
,且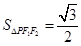 ,
,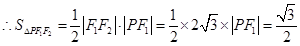 .
.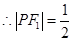 ,
,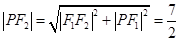 .
.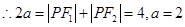 2分
2分又
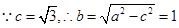 3分
3分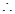 椭圆
椭圆 的方程为
的方程为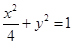 . 4分
. 4分(Ⅱ)由题意知
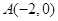 、
、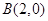 ,
,(1)当直线
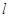 与
与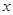 轴垂直时,
轴垂直时,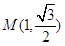 、
、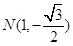 ,则
,则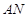 的方程是:
的方程是: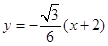 ,
,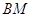 的方程是:
的方程是: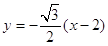 ,直线
,直线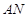 与直线
与直线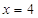 的交点为
的交点为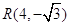 ,
,∴点
 在直线
在直线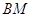 上. 6分
上. 6分(2)当直线
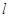 不与
不与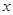 轴垂直时,设直线
轴垂直时,设直线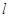 的方程为
的方程为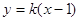 ,
,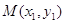 、
、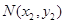 ,
,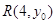
由
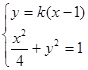 得
得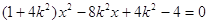
∴
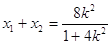 ,
,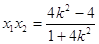 7分
7分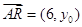 ,
,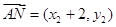 ,
,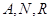 共线,∴
共线,∴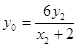 8分
8分又
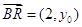 ,
,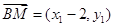 ,需证明
,需证明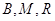 共线,
共线,需证明
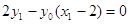 ,只需证明
,只需证明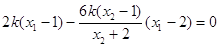
若
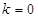 ,显然成立,若
,显然成立,若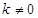 , 即证明
, 即证明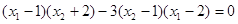
∵
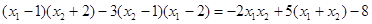
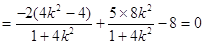 成立, 11分
成立, 11分∴
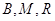 共线,即点
共线,即点 总在直线
总在直线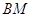 上. 12分
上. 12分
练习册系列答案
相关题目
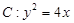 的焦点为
的焦点为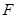 ,过点
,过点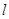 交抛物线
交抛物线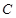 于点
于点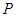 ,
,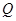 .
.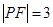 (点
(点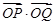 为定值(点
为定值(点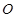 为坐标原点).
为坐标原点). :
: (
( )过点
)过点 ,且椭圆
,且椭圆 .
. 在直线
在直线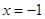 上,过
上,过 两点,且
两点,且 中点,再过
中点,再过 .证明:直线
.证明:直线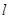 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.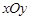 中,已知过点
中,已知过点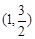 的椭圆
的椭圆 :
: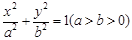 的右焦点为
的右焦点为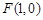 ,过焦点
,过焦点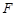 且与
且与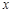 轴不重合的直线与椭圆
轴不重合的直线与椭圆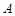 ,
,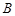 两点,点
两点,点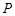 ,直线
,直线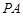 ,
,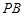 分别交椭圆
分别交椭圆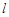 于
于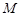 ,
,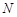 两点.
两点.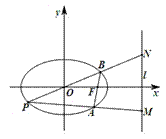
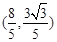 ,试求直线
,试求直线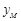 ,
,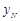 ,试问
,试问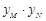 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.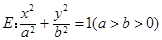 与双曲线
与双曲线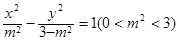 有公共的焦点,过椭圆E的右顶点作任意直线l,设直线l交抛物线
有公共的焦点,过椭圆E的右顶点作任意直线l,设直线l交抛物线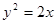 于M、N两点,且
于M、N两点,且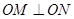 .
.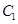 的方程为
的方程为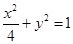 ,双曲线
,双曲线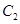 的左、右焦点分别为
的左、右焦点分别为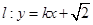 与椭圆
与椭圆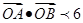 (其中O为原点),求
(其中O为原点),求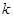 的取值范围。
的取值范围。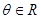 ,则方程
,则方程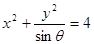 表示的曲线不可能是( )
表示的曲线不可能是( )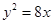 上一点P到y轴的距离为5,则点P到焦点的距离为( )
上一点P到y轴的距离为5,则点P到焦点的距离为( )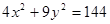 内有一点
内有一点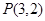 ,过点
,过点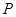 的弦恰好以
的弦恰好以