题目内容
在极坐标系中,圆C1的方程为ρ=4
cos(θ-
),以极点为坐标原点,极轴为x轴的正半轴建立平面坐标系,圆C2的参数方程
(θ为参数),若圆C1与C2相切,则实数a=______.
| 2 |
| π |
| 4 |
|
∵圆C1的方程为ρ=4
cos(θ-
),
∴⊙C1的方程化为ρ=4cosθ+4sinθ,则ρ2=4ρcosθ+4ρsinθ,
由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,得x2+y2-4x-4y=0,
∴圆心C1坐标为(2,2),半径r1=2
,
∵圆C2的参数方程是
,
∴其普通方程是(x+1)2+(y+1)2=a2,
∴以C2的坐标是(-1,-1),r2=|a|,
∵两圆相切,
∴当外切时|C1C2|=|a|+2
=
=3
,解得a=±
,
内切时|C1C2|=|a|-2
=
=3
,解得a=±5
∴a=±
或±5
.
故答案为:±
或±5
.
| 2 |
| π |
| 4 |
∴⊙C1的方程化为ρ=4cosθ+4sinθ,则ρ2=4ρcosθ+4ρsinθ,
由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,得x2+y2-4x-4y=0,
∴圆心C1坐标为(2,2),半径r1=2
| 2 |
∵圆C2的参数方程是
|
∴其普通方程是(x+1)2+(y+1)2=a2,
∴以C2的坐标是(-1,-1),r2=|a|,
∵两圆相切,
∴当外切时|C1C2|=|a|+2
| 2 |
| (2+1)2+(2+1)2 |
| 2 |
| 2 |
内切时|C1C2|=|a|-2
| 2 |
| (2+1)2+(2+1)2 |
| 2 |
| 2 |
∴a=±
| 2 |
| 2 |
故答案为:±
| 2 |
| 2 |

练习册系列答案
相关题目
 中,已知直线
中,已知直线 的参数方程
的参数方程 (
( 为参数),直线
为参数),直线 相交于
相交于 两点,求线段
两点,求线段 的参数方程是( )
的参数方程是( ) (t为参数)
(t为参数)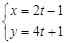 (t为参数)
(t为参数)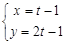 (t为参数)
(t为参数) (
( 为参数)
为参数) 中,以原点O为极点,
中,以原点O为极点, 轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线
轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线 :
: (
( 为参数)和曲线
为参数)和曲线 :
: 上,则
上,则 的最小值为 .
的最小值为 .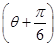 +m=0,曲线C2的参数方程为
+m=0,曲线C2的参数方程为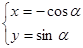 (0<α<π),若曲线C1与C2有两个不同的交点,则实数m的取值范围是____________.
(0<α<π),若曲线C1与C2有两个不同的交点,则实数m的取值范围是____________.