题目内容
数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.令
为公比的等比数列.令![]() ,
,
![]() ,
,![]() .
.
(1)试用![]() 、
、![]() 表示
表示![]() 和
和![]() ;
;
(2)若![]() ,
,![]() 且
且![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
解:(1)当![]() 时,
时,![]() ,
,
![]()
当![]() 时,
时,![]()
![]()
![]()
![]()
所以
 ;
;
(2)因为![]() ,
,
所以![]()
![]()
当![]() 时,
时,![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]()
所以当![]() ,
,![]() 且
且![]() 时,
时,![]() ,即
,即![]() 。
。

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
((本小题满分14分)
数列 是以
是以 为首项,
为首项, 为公比的等比数列.令
为公比的等比数列.令 ,
, ,
, .
.
(1)试用 、
、 表示
表示 和
和 ;
;
(2)若 ,
, 且
且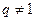 ,试比较
,试比较 与
与 的大小;
的大小;
(3)是否存在实数对 ,其中
,其中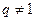 ,使
,使 成等比数列.若存在,求出实数对
成等比数列.若存在,求出实数对 和
和 ;若不存在,请说明理由.
;若不存在,请说明理由.
(本小题满分13分)
随机变量X的分布列如下表如示,若数列 是以
是以 为首项,以
为首项,以 为公比的等比数列,则称随机变量X服从等比分布,记为Q(
为公比的等比数列,则称随机变量X服从等比分布,记为Q( ,
, ).现随机变量X∽Q(
).现随机变量X∽Q( ,2).
,2).
| X | 1 | 2 | … | n |
 |  |  | … |  |
(Ⅱ)一个盒子里装有标号为1,2,…,n且质地相同的标签若干张,从中任取1张标签所得的标号为随机变
 量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不大于3的概率.
量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不大于3的概率.