题目内容
6.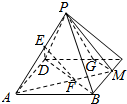 如图,已知点P是平行四边形ABCD所在平面外的一点,E,F分别是PA,BD上的点且PE:EA=BF:FD,延长AF交BC于点M.过M作GM∥BD,且GN交CD于G,求证:平面DEF∥平而PGM.
如图,已知点P是平行四边形ABCD所在平面外的一点,E,F分别是PA,BD上的点且PE:EA=BF:FD,延长AF交BC于点M.过M作GM∥BD,且GN交CD于G,求证:平面DEF∥平而PGM.
分析 由已知条件推导出EF∥PM,FD∥MG,由此能证明平面DEF∥平而PGM.
解答 解:∵四边形ABCD是平行四边形,∴BM∥AD,
∴$\frac{BF}{DF}$=$\frac{MF}{AF}$,
∵E,F分别是PA,BD上的点且PE:EA=BF:FD,延长AF交BC于点M,
∴$\frac{PE}{EA}=\frac{MF}{AF}$,∴EF∥PM,
∵GM∥BD,∴FD∥MG,
∵EF∩FD=F,PM∩MG=M,
EF?平面DEF,FD?平面DEF,PM?平面PGM,MG?平面PGM,
∴平面DEF∥平而PGM.
点评 本题考查面面平行的证明,是基础题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
17.平移坐标轴,将坐标原点移至O′($\sqrt{3}$,1),求下列曲线在新坐标系中的方程:
(1)x=$\sqrt{3}$;
(2)y=4;
(3)(x-2$\sqrt{3}$)2+(y-1)2=2.
(1)x=$\sqrt{3}$;
(2)y=4;
(3)(x-2$\sqrt{3}$)2+(y-1)2=2.
11.已知该球的直径SC=8,A,B是该球球面上的两点,AB=2$\sqrt{3}$,∠SCA=∠SCB=60°,则球心O到平面ABC的距离为( )
| A. | 4$\sqrt{3}$ | B. | $\frac{24\sqrt{13}}{13}$ | C. | $\frac{12\sqrt{13}}{13}$ | D. | 8$\sqrt{3}$ |
 如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.
如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.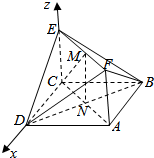 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点,N为AC与BD的交点,求点B到平面CMN的距离.
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点,N为AC与BD的交点,求点B到平面CMN的距离.
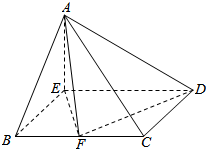 如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.
如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.