题目内容
4.抛物线的焦点在x轴上,抛物线上的点P(-3,m)到焦点的距离为5,则抛物线的标准方程为y2=-8x.分析 由题意可设抛物线的方程为y2=-2px(p>0),其准线方程为x=$\frac{p}{2}$,由抛物线的定义可得,$\frac{p}{2}$-(-3)=5,解得p,进而得到抛物线方程.
解答 解:由题意可设抛物线的方程为y2=-2px(p>0),
其准线方程为x=$\frac{p}{2}$,
由抛物线的定义可得,
抛物线上的点P(-3,m)到焦点的距离为5,
即为P到准线的距离为5,
即有$\frac{p}{2}$-(-3)=5,
解得p=4,
即有抛物线方程为y2=-8x.
故答案为:y2=-8x.
点评 本题考查抛物线的定义、方程和性质,主要考查抛物线的准线方程的运用,注意定义法解题,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知二次函数f(x)=ax2+bx,则“f(2)≥0”是“函数f(x)在(1,+∞)上为增函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.抛物线x2=$\frac{1}{2}$y的准线方程是( )
| A. | x=-$\frac{1}{8}$ | B. | x=$\frac{1}{8}$ | C. | y=-$\frac{1}{8}$ | D. | y=$\frac{1}{8}$ |
13.已知角α的终边经过点A(-$\sqrt{3}$,a),若点A在抛物线y=-$\frac{1}{4}$x2的准线上,则sinα=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
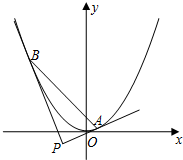 已知抛物线x2=2py(p>0)的焦点F与椭圆$\frac{y^2}{4}$+$\frac{x^2}{3}$=1的一个焦点重合.
已知抛物线x2=2py(p>0)的焦点F与椭圆$\frac{y^2}{4}$+$\frac{x^2}{3}$=1的一个焦点重合. 如图.已知F1,F2分别为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,其离心率e=$\frac{1}{2}$,且a+c=3.
如图.已知F1,F2分别为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,其离心率e=$\frac{1}{2}$,且a+c=3.