题目内容
设锐角△ABC中,2sin2A-cos2A=2.
(1)求∠A的大小;
(2)求(cosB+sinB)2+sin2C的取值范围.
(1)求∠A的大小;
(2)求(cosB+sinB)2+sin2C的取值范围.
(1)由2sin2A-cos2A=2得:cos2A=-
,
因为△ABC是锐角三角形,所以2A∈(0,π),
所以2A=
,所以A=
;
(2)因为C=
-B,
所以(cosB+sinB)2+sin2C
因为△ABC是锐角三角形,A=
,所以B∈(
,
)
所以2B-
∈(
,
),
所以(cosB-sinB)2+sin2C的取值范围是(1+
,1+
].
| 1 |
| 2 |
因为△ABC是锐角三角形,所以2A∈(0,π),
所以2A=
| 2π |
| 3 |
| π |
| 3 |
(2)因为C=
| 2π |
| 3 |
所以(cosB+sinB)2+sin2C
|
因为△ABC是锐角三角形,A=
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
所以2B-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
所以(cosB-sinB)2+sin2C的取值范围是(1+
| ||
| 2 |
| 3 |

练习册系列答案
相关题目
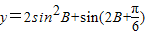 取最大值时,∠B的大小.
取最大值时,∠B的大小.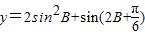 取最大值时,∠B的大小.
取最大值时,∠B的大小.