题目内容
设锐角△ABC中,角ABC对边分别为a、b、c,且b=2asinB
(1)求角A的大小;(2)若a=2,求△ABC的面积的最大值.
(1)求角A的大小;(2)若a=2,求△ABC的面积的最大值.
分析:(1)由b=2asinB结合正弦定理可得sinB=2sinAsinB可求sinA,进而可求A
(2)由余弦定理可得a2=b2+c2-2bccosA=b2+c2-
bc≥2bc-
bc,从而可得bc的范围,代入面积公式S△ABC=
bcsinA可求△ABC面积最大值
(2)由余弦定理可得a2=b2+c2-2bccosA=b2+c2-
| 3 |
| 3 |
| 1 |
| 2 |
解答:解:(1)∵b=2asinB
∴sinB=2sinAsinB
得:sinA=
即A=
(2)∵a2=b2+c2-2bccosA=b2+c2-
bc≥2bc-
bc
∴bc≤
=4(2+
)
当且仅当b=c=
+
时取等号
S△ABC=
bcsinA≤
×4(2+
)×
=2+
即△ABC面积最大值为2+
(当且仅当b=c=
+
时取等号)
∴sinB=2sinAsinB
得:sinA=
| 1 |
| 2 |
| π |
| 6 |
(2)∵a2=b2+c2-2bccosA=b2+c2-
| 3 |
| 3 |
∴bc≤
| 4 | ||
2-
|
| 3 |
当且仅当b=c=
| 6 |
| 2 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
即△ABC面积最大值为2+
| 3 |
| 2 |
| 6 |
点评:本题主要考查了正弦定理与余弦定理及三角形的面积公式的综合应用,解题的关键是应用了基本不等式.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、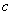 ,且
,且 。(1)求角
。(1)求角