题目内容
已知数列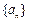 的前n项和
的前n项和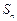 满足:
满足: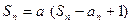 (
(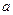 为常数,
为常数,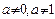 )(Ⅰ)求
)(Ⅰ)求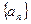 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设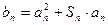 ,若数列
,若数列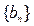 为等比数列,求
为等比数列,求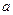 的值;(Ⅲ)在满足条件(Ⅱ)的情形下,
的值;(Ⅲ)在满足条件(Ⅱ)的情形下,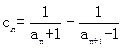 ,数列
,数列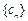 的前n项和为
的前n项和为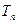 . 求证:
. 求证: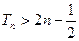 .
.
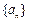 的前n项和
的前n项和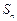 满足:
满足: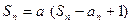 (
(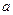 为常数,
为常数,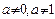 )(Ⅰ)求
)(Ⅰ)求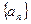 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设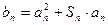 ,若数列
,若数列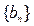 为等比数列,求
为等比数列,求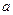 的值;(Ⅲ)在满足条件(Ⅱ)的情形下,
的值;(Ⅲ)在满足条件(Ⅱ)的情形下,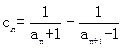 ,数列
,数列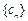 的前n项和为
的前n项和为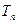 . 求证:
. 求证: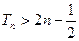 .
.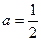
解:(Ⅰ)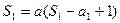
∴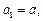 ……….1分
……….1分
当 时,
时,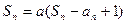 ,
,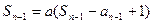 ,两式相减得:
,两式相减得: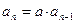 ,
,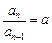
(a≠0,n≥2)即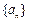 是等比数列.∴
是等比数列.∴ ;…4分
;…4分
(Ⅱ)由(Ⅰ)知a≠1,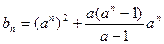 ,
,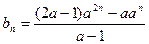 ,
,
若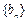 为等比数列,则有
为等比数列,则有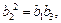 而
而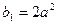 ,
,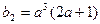 ,
,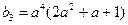 …6分
…6分
故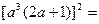
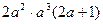 ,解得
,解得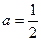 , ……………………7分
, ……………………7分
再将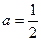 代入得
代入得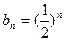 成立,所以
成立,所以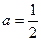 . …………8分
. …………8分
(III)证明:由(Ⅱ)知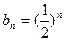 ,所以
,所以
 ,
,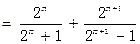
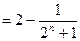
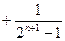 … 10分
… 10分
所以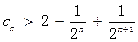

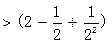
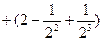
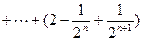

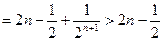 ………12分
………12分
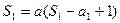
∴
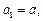 ……….1分
……….1分当
 时,
时,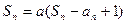 ,
,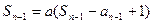 ,两式相减得:
,两式相减得: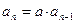 ,
,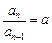
(a≠0,n≥2)即
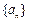 是等比数列.∴
是等比数列.∴ ;…4分
;…4分(Ⅱ)由(Ⅰ)知a≠1,
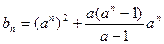 ,
,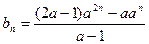 ,
,若
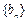 为等比数列,则有
为等比数列,则有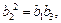 而
而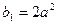 ,
,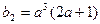 ,
,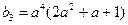 …6分
…6分故
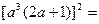
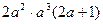 ,解得
,解得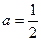 , ……………………7分
, ……………………7分再将
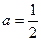 代入得
代入得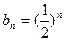 成立,所以
成立,所以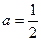 . …………8分
. …………8分(III)证明:由(Ⅱ)知
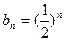 ,所以
,所以
 ,
,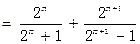
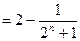
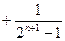 … 10分
… 10分所以
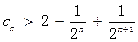

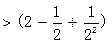
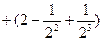
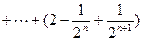

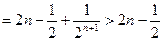 ………12分
………12分
练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
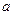 ,都存在正整数
,都存在正整数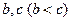 ,使得
,使得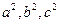 成等差数列;
成等差数列;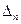 ,其边长
,其边长 为正整数且
为正整数且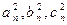 成等差数列.
成等差数列. 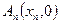 满足:
满足: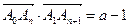 (其中
(其中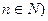 ,又知
,又知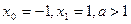 .
. 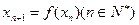 ,求
,求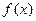 的表达式;
的表达式; 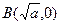 记
记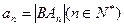 ,且
,且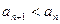 对一切
对一切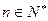 恒成立,试求
恒成立,试求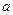 的取值范围;
的取值范围;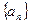 的前
的前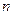 项和为
项和为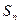 ,试证:
,试证: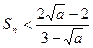 .
. 为等差数列,
为等差数列,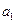 +
+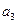 +
+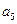 =105,
=105, =99,以
=99,以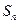 表示
表示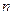 项和,则使得
项和,则使得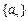 的前
的前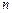 项和为
项和为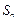 ,若
,若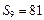 ,则
,则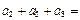 .
.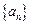 的通项公式为
的通项公式为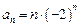 ,则数列
,则数列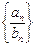 成等比数列是数列
成等比数列是数列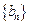 的通项公式为
的通项公式为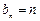 的( ▲ )
的( ▲ )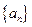 中
中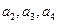 分别是某等差数列的第5项、第3 项、第2项,且
分别是某等差数列的第5项、第3 项、第2项,且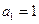 公比
公比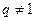 ,则
,则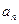 等于( )
等于( )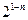
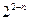
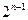
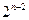
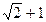 与
与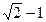 两数的等差中项是
两数的等差中项是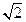
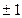
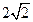
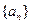 ,
,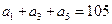 ,
,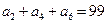 . 以
. 以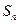 表示
表示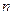 项和,则使得
项和,则使得