Question

（09年西城区抽样理）（14分）

已知的顶点A在射线上， A, B两点关于x轴对称，O为坐标原点，且线段AB上有一点M满足. 当点A在l上移动时，记点M的轨迹为W.

    (Ⅰ) 求轨迹W的方程；

    (Ⅱ)设P(-1,0)，Q(2,0)，求证：.

Answer 1

 解析：（Ⅰ）解：因为A, B两点关于x轴对称，

所以AB边所在直线与y轴平行.                            

设M(x, y)，由题意，得，           ----------------------2分

     所以，                    

因为，

所以，即，     ------------------------5分

所以点M的轨迹W的方程为.            ------------------6分

（Ⅱ）证明：设，

     因为曲线关于x轴对称，

     所以只要证明“点M在x轴上方及x轴上时，”成立即可.

     以下给出“当时，” 的证明过程.     

因为点M在上，所以.

当x₀=2时，由点M在W上，得点，

          此时，

          所以，则；  --------------8分

     当时，直线PM、QM的斜率分别为，

          因为，所以，且，

          又，所以，且，   

    所以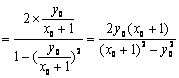，--10分

    因为点M在W上，所以，即，

    所以，

    因为，

    所以，                     --------------------12分

    在中，因为，且，，

    所以.                             

综上，得当时，.

所以对于轨迹W的任意一点M，成立.   --------------------14分