题目内容
(09年西城区抽样理)(14分)
已知f是直角坐标平面xOy到自身的一个映射,点![]() 在映射f下的象为点
在映射f下的象为点![]() ,记作
,记作![]() .
.
设![]()
![]() ,
,![]() ,
,![]() . 如果存在一个圆,使所有的点
. 如果存在一个圆,使所有的点![]() 都在这个圆内或圆上,那么称这个圆为点
都在这个圆内或圆上,那么称这个圆为点![]() 的一个收敛圆. 特别地,当
的一个收敛圆. 特别地,当![]() 时,则称点
时,则称点![]() 为映射f下的不动点.
为映射f下的不动点.
(Ⅰ) 若点![]() 在映射f下的象为点
在映射f下的象为点![]() .
.
1 求映射f下不动点的坐标;
2 若![]() 的坐标为(1,2),判断点
的坐标为(1,2),判断点![]() 是否存在一个半径为3的收敛圆,并说明理由.
是否存在一个半径为3的收敛圆,并说明理由.
解析:(Ⅰ)1解:设不动点的坐标为![]() ,
,
由题意,得![]() ,解得
,解得![]() ,
,
所以映射f下不动点为![]() . -------------------2分
. -------------------2分
2结论:点![]() 不存在一个半径为3的收敛圆.
不存在一个半径为3的收敛圆.
证明:由![]() ,得
,得![]() ,
,
所以![]() ,
,
则点![]() 不可能在同一个半径为3的圆内,
不可能在同一个半径为3的圆内,
所以点![]()
![]() N*)不存在一个半径为3的收敛圆. ------------------5分
N*)不存在一个半径为3的收敛圆. ------------------5分
(Ⅱ)证明:由![]() ,得
,得![]() .
.
由![]() ,得
,得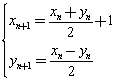 ,
, ![]() ---------------7分
---------------7分
所以![]() ,
,
由![]() ,得
,得 ,
,
所以![]() , ------------------9分
, ------------------9分
即![]() ,
,
由![]() ,得
,得![]() ,同理
,同理![]() ,
,
所以![]() ,
,
所以数列![]() N*)都是公比为
N*)都是公比为![]() 的等比数列,首项分别为
的等比数列,首项分别为
![]() ,
,
所以![]() ,
,
同理可得![]() . ------------------12分
. ------------------12分
所以对任意![]() N*,
N*,![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
,
故所有的点![]() 都在以
都在以![]() 为圆心,
为圆心,![]() 为半径的圆内或圆上,
为半径的圆内或圆上,

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案