题目内容
如图，P﹣ABCD是正四棱锥，
，AB=2．
（1）求证：平面PAC⊥平面PBD；
（2）求该四棱锥的体积．
解答：
（1）证明：设AC∩BD=O，连接PO…（1分），
因为P﹣ABCD是正四棱锥，所以AC⊥BD，PO⊥AC…（3分），
因为PO∩BD=O，所以AC⊥平面PBD…（5分），
因为AC⊂平面PAC，所以平面PAC⊥平面PBD…（7分）
（2）解：因为AB=2，所以
…（8分），
所以
…（9分），
因为P﹣ABCD是正四棱锥，所以PO⊥平面ABCD…（10分）
所以，该四棱锥的体积
…（13分）（每个等号1分）．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
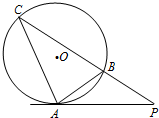（2013•深圳二模）如图，P是⊙O外一点，PA与⊙O相切于点A，割线PC与⊙O相交于点B，C，且PA=3，PC=3
选做题：请考生在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分．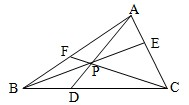
如图，P是△ABC内一点，BP、CP、AP的延长线分别与AC、AB、BC交于点E、F、D．考虑下列三个等式：