题目内容
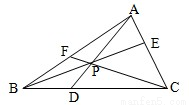
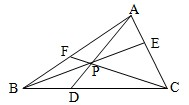 如图,P是△ABC内一点,BP、CP、AP的延长线分别与AC、AB、BC交于点E、F、D.考虑下列三个等式:
如图,P是△ABC内一点,BP、CP、AP的延长线分别与AC、AB、BC交于点E、F、D.考虑下列三个等式:(1)
| S△ABP |
| S△APC |
| BD |
| CD |
(2)
| S△BPC+S△APC |
| S△APC |
| AB |
| BF |
(3)
| CE |
| AE |
| AB |
| BF |
| FP |
| PC |
其中正确的有( )
分析:根据等高不等底的三角形的面积的比等于底边的比和等式的性质求解,判断正确选项即可.
解答:解:由图形在△ABC中,可得:
=
,
在△PBC中,
=
,
∴
=
=
,
∴①正确;
=
+
=
+1,
由①
=
,所以
=
,
∴
=
+1=
.
∴②正确;
×
×
=
×
×
=1.
∴③正确.
故①②③都正确.
故选A.
| S△ABD |
| S△ADC |
| BD |
| CD |
在△PBC中,
| S△BDP |
| S△CPD |
| BD |
| CD |
∴
| S△ABP |
| S△APC |
| ||
|
| BD |
| CD |
∴①正确;
| S△BPC+S△APC |
| S△APC |
| S△BPC |
| S△APC |
| S△APC |
| S△APC |
| S△BPC |
| S△APC |
由①
| S△ABP |
| S△APC |
| BD |
| CD |
| S△BPC |
| S△APC |
| AF |
| BF |
∴
| S△BPC+S△APC |
| S△APC |
| AF |
| BF |
| AB |
| BF |
∴②正确;
| CE |
| AE |
| AB |
| BF |
| FP |
| PC |
| S△BPC |
| S△APB |
| S△APB |
| S△BFP |
| S△BFP |
| S△BPC |
∴③正确.
故①②③都正确.
故选A.
点评:本题考查三角形面积的知识,难度较大,关键是根据等高不等底的三角形的面积的比等于底边的比求解.

练习册系列答案
相关题目
 如图,P是△ABC所在的平面内一点,且满足
如图,P是△ABC所在的平面内一点,且满足 如图,P是△ABC内一点,BP、CP、AP的延长线分别与AC、AB、BC交于点E、F、D.考虑下列三个等式:
如图,P是△ABC内一点,BP、CP、AP的延长线分别与AC、AB、BC交于点E、F、D.考虑下列三个等式: ;
;  ;
; .
.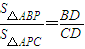 ;
; 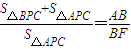 ;
;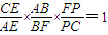 .
.
 ,则
,则 



