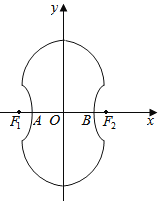题目内容
【题目】在平面直角坐标系![]() 中,
中,![]() 经过原点的直线
经过原点的直线![]() 将
将![]() 分成左、右两部分,记左、右两部分的面积分别为
分成左、右两部分,记左、右两部分的面积分别为![]() ,则
,则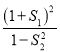 取得最小值时,直线
取得最小值时,直线![]() 的斜率( )
的斜率( )
A.等于1B.等于![]() C.等于
C.等于![]() D.不存在
D.不存在
【答案】D
【解析】
方法一:根据四个选项可知,分别计算![]() ,
,![]() ,
,![]() ,和
,和![]() 不存在时
不存在时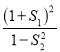 的值,比较大小即可;
的值,比较大小即可;
方法二:讨论斜率![]() ,
,![]() ,
,![]() 不存在三种情况,在三种情况下分别求出
不存在三种情况,在三种情况下分别求出![]() ,代入表达式
,代入表达式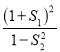 ,化简比较大小即可.
,化简比较大小即可.
方法一:因为,![]()
所以![]()
当![]() 时,
时,![]() ,此时
,此时![]() ,
,![]() ,∴
,∴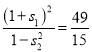
当![]() 时,
时, ![]() ,此时,
,此时,![]() ,
,![]() ,∴
,∴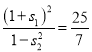
当![]() 时,
时, ![]() ,此时,
,此时, ![]() ,
,![]() ,∴
,∴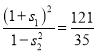
当![]() 不存在时,
不存在时, ![]() ,此时,
,此时, ![]() ,∴
,∴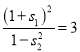
综上比较可知,当![]() 不存在时,
不存在时, 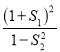 的值最小
的值最小
故选:D
方法二: 因为,![]()
所以![]()
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]()
直线![]() 的方程为
的方程为![]()
此时直线与![]() 相交,设交点为E,则
相交,设交点为E,则![]()
解方程可得E点坐标为![]()
则![]()
所以![]()
则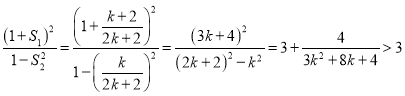
当![]() 时, 直线
时, 直线![]() 的方程为
的方程为![]()
直线![]() 的方程为
的方程为![]()
此时直线与![]() 相交,设交点为F,则
相交,设交点为F,则![]()
解方程可得F点坐标为![]()
则![]()
所以![]()
则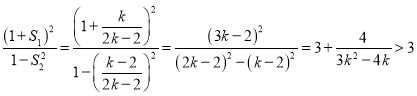
当![]() 不存在时
不存在时![]() ,此时,
,此时, ![]() ,∴
,∴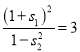
综上可知, 当![]() 不存在时,
不存在时, 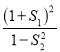 的值最小
的值最小
故选:D

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目