题目内容
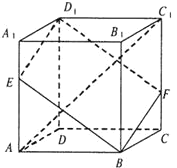
【题目】如图，在棱长为3的正方体
中，
．
求两条异面直线
与
所成角的余弦值；
求直线与平面
所成角的正弦值．
【答案】（1）
（2）
【解析】
（1）以D为原点，建立空间直角坐标系D-xyz，则我们易求出已知中，各点的坐标，进而求出向量
，
的坐标．代入向量夹角公式，结合异面直线夹角公式，即可得到答案．
（2）设出平面BED1F的一个法向量为
，根据法向量与平面内任一向量垂直，数量积为0，构造方程组，求出平面BED1F的法向量为的坐标，代入线面夹角向量公式，即可求出答案．
解：（1）以D为原点，建立空间直角坐标系D-xyz如图所示：
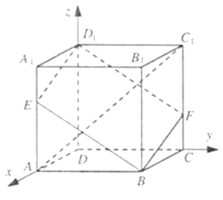
则A（3，0，0），C1=（0，3，3），D1=（0，0，3），E（3，0，2）
∴=（-3，3，3），=（3，0，-1）
∴cosθ=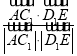
=
=-
则两条异面直线AC1与D1E所成角的余弦值为
（2）B（3，3，0），
=（0，-3，2），=（3，0，-1）
设平面BED1F的一个法向量为=（x，y，z）
由
得
令x=1，则=（1，2，3）
则直线AC1与平面BED1F所成角的正弦值为
|
|=
=
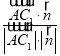练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
