题目内容
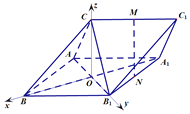
【题目】如图,三棱柱![]() 中,M,N分别为
中,M,N分别为![]() 的中点.
的中点.
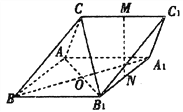
(1)证明:直线MN//平面CAB1;
(2)若四边形ABB1A1是菱形,且![]() ,
, ![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
【答案】(1)见解析;(2)余弦值为![]() .
.
【解析】试题分析:
(1)由题意结合几何关系可证得![]() ,利用线面平行的判定定理可证得直线MN//平面CAB1;
,利用线面平行的判定定理可证得直线MN//平面CAB1;
(2)结合几何体的特征建立空间直角坐标系,利用半平面的法向量可求得平面![]() 和平面
和平面![]() 所成的角(锐角)的余弦值为
所成的角(锐角)的余弦值为![]() .
.
试题解析:
(1)设![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,
因为四边形![]() 是平行四边形,所以是
是平行四边形,所以是![]() 是
是![]() 的中点,
的中点,
![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
又因为![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
所以![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以直线![]() 平面
平面![]() .
.
(2)因为平行四边形![]() 是菱形,所以
是菱形,所以![]() .
.
又因为![]() ,所以
,所以![]() .又
.又![]() 且
且![]() 是
是![]() 的中点,所以
的中点,所以![]() .又因为
.又因为![]() ,所以
,所以![]() ≌
≌![]() ,所以
,所以![]() ,故
,故![]() ,从而
,从而![]() 两两垂直. 以
两两垂直. 以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴建立如图空间直角坐标系
轴建立如图空间直角坐标系![]() ,
,
则![]() ,
, ![]() ,
,
![]() ,
, ![]()
因为![]() 两两垂直,所以
两两垂直,所以![]() 平面
平面![]() ,
,
所以![]() 是平面
是平面![]() 的一个法向量;
的一个法向量;
设![]()
![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则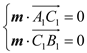 ,即
,即 ,
,
令![]() ,得
,得![]() ,所以
,所以![]()
所以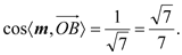
所以平面![]() 和平面
和平面![]() 所成的角(锐角)的余弦值为
所成的角(锐角)的余弦值为![]()

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
【题目】今有一组数据如下表:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 90 | 84 | 83 | m | 75 | 68 |
由最小二乘法求得点![]()
![]() 的回归直线方程是
的回归直线方程是![]() ,其中
,其中![]() .
.
(Ⅰ)求m的值,并求回归直线方程;
(Ⅱ)设![]() ,我们称
,我们称![]() 为点
为点![]() 的残差,记为
的残差,记为![]() .
.
从所给的点![]()
![]() 中任取两个,求其中有且只有一个点的残差绝对值不大于1的概率.
中任取两个,求其中有且只有一个点的残差绝对值不大于1的概率.
参考公式:  .
.