Question

【题目】已知E，F分别是棱长为1的正方体ABCD﹣A1B1C1D1的棱BC，CC1的中点，则截面AEFD1与底面ABCD所成二面角的正弦值是 ．

Answer 1

【答案】
【解析】解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，
A（1，0，0），E（ ,1,0），F（0，1， ），
=（﹣ ，1，0）， =（﹣1，1， ），
设平面AEFD1的法向量 =（x，y，z），
则 ，取x=2，得 =（2，1，2），
平面ABCD的法向量 =（0，0，1），
截面AEFD1与底面ABCD所成二面角为θ，
cosθ= = ，
∴sinθ= = ．
∴截面AEFD1与底面ABCD所成二面角的正弦值是 ．
故答案为： ．

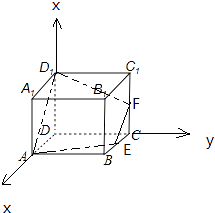
以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，利用向量法能求出截面AEFD1与底面ABCD所成二面角的正弦值．