题目内容
已知数列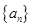 满足:
满足: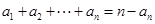 ,其中
,其中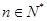 .
.
(1)求证:数列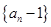 是等比数列;
是等比数列;
(2)令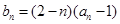 ,求数列
,求数列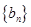 的最大项.
的最大项.
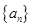 满足:
满足: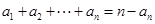 ,其中
,其中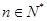 .
.(1)求证:数列
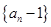 是等比数列;
是等比数列;(2)令
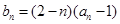 ,求数列
,求数列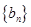 的最大项.
的最大项.(1)详见解析;(2)最大项为 .
.
 .
.试题分析:(1)首先根据已知等式
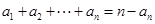 ,令
,令 ,可得
,可得 ,再根据已知等式可得
,再根据已知等式可得 ,将两式相减,即可得到数列
,将两式相减,即可得到数列 的一个递推公式,只需验证将此递推公式变形得到形如
的一个递推公式,只需验证将此递推公式变形得到形如 的形式,从可证明数列
的形式,从可证明数列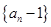 是等比数列;(2)由(1)可得
是等比数列;(2)由(1)可得 ,从而
,从而 ,因此要求数列
,因此要求数列 的最大项,可以通过利用作差法判断数列
的最大项,可以通过利用作差法判断数列 的单调性来求得:
的单调性来求得: ,
,当
 时,
时, ,即
,即 ;当
;当 时,
时, ; 当
; 当 时,
时, ,即
,即 ,因此数列
,因此数列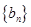 的最大项为
的最大项为 .
.试题解析:(1)当
 时,
时, ,∴
,∴ , 1分
, 1分又∵
 , 2分
, 2分∴
 ,即
,即 ,∴
,∴ . 4分
. 4分又∵
 ,∴数列
,∴数列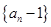 是首项为
是首项为 ,公比为
,公比为 的等比数列; 6分
的等比数列; 6分(2)由(1)知,
 ,
,∴
 , ∴
, ∴ , 8分
, 8分当
 时,
时, ,即
,即 , 9分
, 9分当
 时,
时, , 10分
, 10分 当
 时,
时, ,即
,即 , 11分
, 11分∴数列
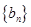 的最大项为
的最大项为 , 13分
, 13分
练习册系列答案
相关题目
 的首项
的首项 ,
, ,
, ,
, 为等比数列;
为等比数列; ,求最大的正整数
,求最大的正整数 .
.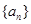 的首项
的首项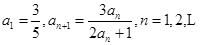 .
.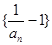 是等比数列,并求出
是等比数列,并求出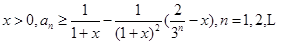 ;
;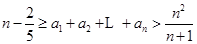 .
.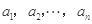 .对
.对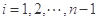 ,该数列前
,该数列前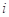 项的最大值记为
项的最大值记为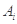 ,后
,后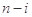 项
项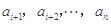 的最小值记为
的最小值记为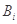 ,
,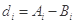 .
.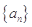 为3,4,7,1,写出
为3,4,7,1,写出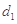 ,
,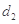 ,
,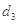 的值;
的值;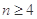 )是公比大于1的等比数列,且
)是公比大于1的等比数列,且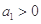 .证明:
.证明: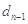 是等比数列.
是等比数列.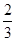 的等比数列
的等比数列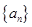 的前
的前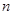 项和为
项和为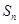 ,则 ( )
,则 ( )



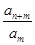 =an,则a3=________;{an}的前n项和Sn=________.
=an,则a3=________;{an}的前n项和Sn=________.