题目内容
给定数列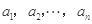 .对
.对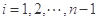 ,该数列前
,该数列前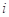 项的最大值记为
项的最大值记为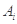 ,后
,后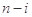 项
项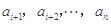 的最小值记为
的最小值记为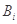 ,
,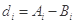 .
.
(1)设数列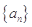 为3,4,7,1,写出
为3,4,7,1,写出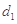 ,
,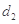 ,
,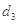 的值;
的值;
(2)设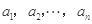 (
(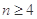 )是公比大于1的等比数列,且
)是公比大于1的等比数列,且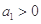 .证明:
.证明: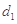 ,
,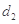 ,…,
,…,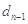 是等比数列.
是等比数列.
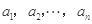 .对
.对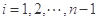 ,该数列前
,该数列前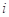 项的最大值记为
项的最大值记为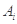 ,后
,后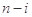 项
项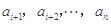 的最小值记为
的最小值记为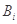 ,
,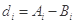 .
.(1)设数列
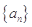 为3,4,7,1,写出
为3,4,7,1,写出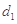 ,
,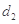 ,
,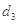 的值;
的值;(2)设
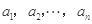 (
(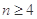 )是公比大于1的等比数列,且
)是公比大于1的等比数列,且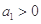 .证明:
.证明: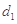 ,
,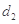 ,…,
,…,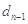 是等比数列.
是等比数列.(1) ;(2)
;(2) ,即证明是等比数列.
,即证明是等比数列.
 ;(2)
;(2) ,即证明是等比数列.
,即证明是等比数列.试题分析:解题思路:(1)利用所给定义,依次求
 即可(2)设法证明
即可(2)设法证明 即可.规律总结:凡是新定义性题目,要阅读定义中的信息,与已学知识点相结合,使之转化为学过的知识是解决本类题目的关键.
即可.规律总结:凡是新定义性题目,要阅读定义中的信息,与已学知识点相结合,使之转化为学过的知识是解决本类题目的关键.试题解析:(1)
 .
.(2)因为
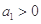 ,公比
,公比 ,所以
,所以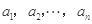 是递增数列.
是递增数列. 因此,对
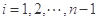 ,
, ,
, .
. 于是对
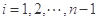 ,
, .
. 因此
 且
且 (
( ),即
),即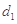 ,
,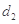 ,,
,,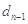 是等比数列.
是等比数列. 
练习册系列答案
相关题目
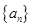 满足:
满足: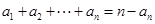 ,其中
,其中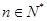 .
.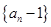 是等比数列;
是等比数列;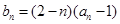 ,求数列
,求数列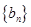 的最大项.
的最大项.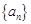 满足
满足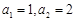 ,
,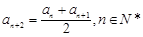 .
.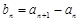 ,证明:
,证明: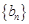 是等比数列;
是等比数列; 中,
中, (c为非零常数)且前n项和
(c为非零常数)且前n项和 ,则实数k等于( ).
,则实数k等于( ). 1
1 中的内角
中的内角 所对的边分别为
所对的边分别为 ,若
,若
 成等比数列,则
成等比数列,则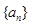 中,
中,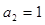 ,则其前
,则其前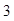 项的和
项的和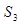 的取值范围是 ( )
的取值范围是 ( ) 



 ,把数列
,把数列 的各项排列成如下的三角形状,
的各项排列成如下的三角形状,




 中,
中, ,
, ,则
,则 的值 ( )
的值 ( )
