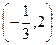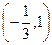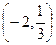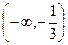题目内容
(本题满分12分)若实数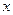 、
、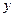 、
、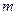 满足
满足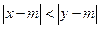 ,则称
,则称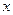 比
比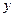 接近
接近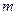 .
.
(1)若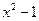 比3接近0,求
比3接近0,求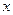 的取值范围;
的取值范围;
(2)对任意两个不相等的正数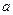 、
、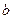 ,证明:
,证明: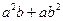 比
比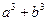 接近
接近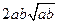 ;
;
(3)已知函数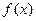 的定义域
的定义域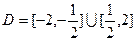 .任取
.任取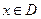 ,
,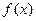 等于
等于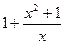 和
和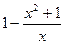 中接近0的那个值.写出函数
中接近0的那个值.写出函数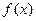 的解析式,并指出它的奇偶性、最值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最值和单调性(结论不要求证明).
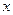 、
、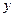 、
、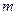 满足
满足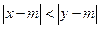 ,则称
,则称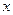 比
比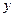 接近
接近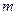 .
.(1)若
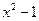 比3接近0,求
比3接近0,求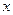 的取值范围;
的取值范围;(2)对任意两个不相等的正数
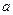 、
、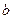 ,证明:
,证明: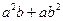 比
比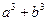 接近
接近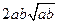 ;
;(3)已知函数
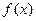 的定义域
的定义域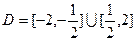 .任取
.任取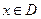 ,
,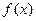 等于
等于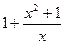 和
和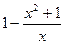 中接近0的那个值.写出函数
中接近0的那个值.写出函数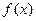 的解析式,并指出它的奇偶性、最值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最值和单调性(结论不要求证明).(1)xÎ(-2,2);
(2)略
(3)f(x)是偶函数;函数f(x)的最小值为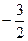 ,最大值为
,最大值为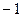 ;
;
函数f(x)在区间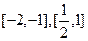 单调递增,在区间
单调递增,在区间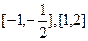 单调递减.
单调递减.
(2)略
(3)f(x)是偶函数;函数f(x)的最小值为
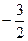 ,最大值为
,最大值为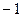 ;
;函数f(x)在区间
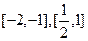 单调递增,在区间
单调递增,在区间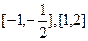 单调递减.
单调递减.解:(1) xÎ(-2,2);
(2) 对任意两个不相等的正数a、b,有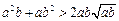 ,
,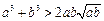 ,
,
因为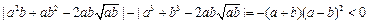 ,
,
所以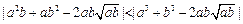 ,即a2b+ab2比a3+b3接近
,即a2b+ab2比a3+b3接近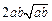 ;
;
(3)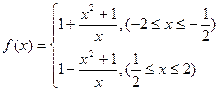 =
=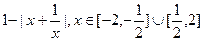 ,
,
f(x)是偶函数;函数f(x)的最小值为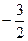 ,最大值为
,最大值为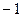 ;
;
函数f(x)在区间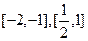 单调递增,在区间
单调递增,在区间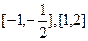 单调递减.
单调递减.
(2) 对任意两个不相等的正数a、b,有
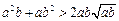 ,
,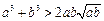 ,
,因为
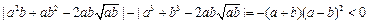 ,
,所以
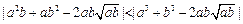 ,即a2b+ab2比a3+b3接近
,即a2b+ab2比a3+b3接近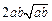 ;
;(3)
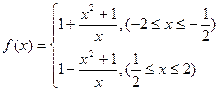 =
=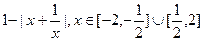 ,
,f(x)是偶函数;函数f(x)的最小值为
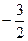 ,最大值为
,最大值为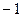 ;
;函数f(x)在区间
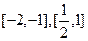 单调递增,在区间
单调递增,在区间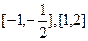 单调递减.
单调递减.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
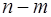 表示
表示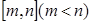 的区间长度,函数
的区间长度,函数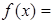
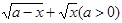 的值域区间长度为
的值域区间长度为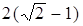 ,则实数
,则实数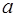 的值是( )
的值是( )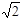
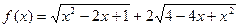 .
.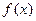 的值域;
的值域; 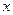 的不等式
的不等式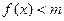 有解,求实数
有解,求实数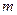 的范围.
的范围.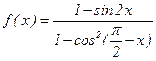
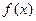 的定义域; (2)已知
的定义域; (2)已知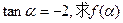 的值.
的值.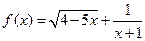 的定义域为____________________________.
的定义域为____________________________.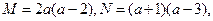 则有()
则有()
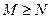 (等号定能取到)
(等号定能取到)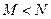
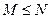 (等号定能取到)
(等号定能取到)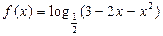 的值域为( )
的值域为( ) 
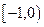
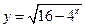 的值域是( )
的值域是( )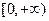
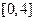
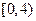
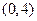
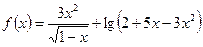 的定义域是 ( )
的定义域是 ( )