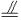题目内容
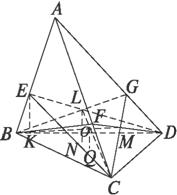
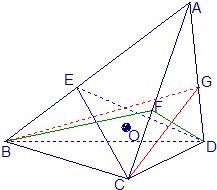 如图,在体积为1的三棱锥A-BCD侧棱AB、AC、AD上分别取点E、F、G,使AE:EB=AF:FC=AG:GD=2:1,记O为三平面BCG、CDE、DBF的交点,则三棱锥O-BCD的体积等于( )
如图,在体积为1的三棱锥A-BCD侧棱AB、AC、AD上分别取点E、F、G,使AE:EB=AF:FC=AG:GD=2:1,记O为三平面BCG、CDE、DBF的交点,则三棱锥O-BCD的体积等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:画出图形,三棱锥O-BCD的体积,转化为线段的长度比,充分利用直线的平行进行推到,求出比例即可.
解答: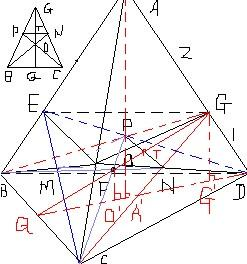 解:AA'为正三棱锥A-BCD的高;OO'为正三棱锥O-BCD的高
解:AA'为正三棱锥A-BCD的高;OO'为正三棱锥O-BCD的高
因为底面△BCD相同,则它们的体积比为高之比
已知三棱锥A-BCD的体积为1
所以,三棱锥O-BCD的体积为:
…(1)
由前面知,FG∥CD且
=
所以由平行得到,
=
=
所以,
=
[面BCG所在的平面图如左上角简图]
同理,
=
则,
=
所以,PN∥BC
那么,
=
=
亦即,
=
=
设GQ=x
那么,GT=
x
则,QT=GQ-GT=x-
=
而,
=
=
=
所以:
=
则,TO=
QT=
×
x=
所以:GO=GT+TO=
x+
=
所以,OQ=GQ-GO=x-
=
又,
=
所以,
=
=
…(2)
且,
=
所以:
=
…(3)
由(2)*(3)得到:
=
×
=
代入到(1)得到:
三棱锥O-BCD的体积就是
=
 解:AA'为正三棱锥A-BCD的高;OO'为正三棱锥O-BCD的高
解:AA'为正三棱锥A-BCD的高;OO'为正三棱锥O-BCD的高因为底面△BCD相同,则它们的体积比为高之比
已知三棱锥A-BCD的体积为1
所以,三棱锥O-BCD的体积为:
| OO′ |
| AA′ |
由前面知,FG∥CD且
| FG |
| CD |
| 2 |
| 3 |
所以由平行得到,
| FG |
| CD |
| GN |
| NC |
| 2 |
| 3 |
| GN |
| GC |
| 2 |
| 5 |
同理,
| GP |
| GB |
| 2 |
| 5 |
则,
| GN |
| GC |
| GP |
| GB |
所以,PN∥BC
那么,
| PN |
| BC |
| GN |
| GC |
| 2 |
| 5 |
| GT |
| GQ |
| GN |
| GC |
| 2 |
| 5 |
那么,GT=
| 2 |
| 5 |
则,QT=GQ-GT=x-
| 2x |
| 5 |
| 3x |
| 5 |
| TO |
| OQ |
| TN |
| BQ |
| GN |
| GC |
| 2 |
| 5 |
| TO |
| TQ |
| 2 |
| 7 |
则,TO=
| 2 |
| 7 |
| 2 |
| 7 |
| 3 |
| 5 |
| 6x |
| 35 |
所以:GO=GT+TO=
| 2 |
| 5 |
| 6x |
| 35 |
| 4x |
| 7 |
| 4x |
| 7 |
| 3x |
| 7 |
又,
| OQ |
| GQ |
| OO′ |
| GG′ |
所以,
| OO′ |
| GG′ |
| ||
| x |
| 3 |
| 7 |
且,
| DG |
| DA |
| GG′ |
| AA′ |
所以:
| GG′ |
| AA′ |
| 1 |
| 3 |
由(2)*(3)得到:
| OO′ |
| AA′ |
| 3 |
| 7 |
| 1 |
| 3 |
| 1 |
| 7 |
三棱锥O-BCD的体积就是
| OO′ |
| AA′ |
| 1 |
| 7 |
点评:本题考查学生对三棱锥的认识,以及必要的辅助线的作法,是难题.

练习册系列答案
相关题目
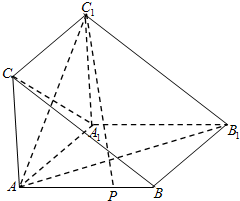 如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC⊥AB,AC=AA1=1,P为线段AB上的动点.
如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC⊥AB,AC=AA1=1,P为线段AB上的动点.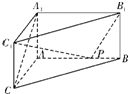 (2012•蓝山县模拟)如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥AC,AC=AA1=1,P为线段AB上的动点.
(2012•蓝山县模拟)如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥AC,AC=AA1=1,P为线段AB上的动点.