Question

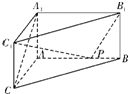（2012•蓝山县模拟）如图，在体积为1的三棱柱ABC-A₁B₁C₁中，侧棱AA₁⊥底面ABC，AB⊥AC，AC=AA₁=1，P为线段AB上的动点．
（1）求证：CA₁⊥C₁P；
（2）当AP为何值时，二面角C₁-PB₁-A₁的大小为

π

6

？

Answer 1

分析：（1）先以A为原点，AC，AB，AA₁所在的直线分别为x轴，y轴，z轴建立直角坐标系，求出各点的坐标以及对应向量的坐标，进而得到

CA1

•

C1P

=0即可得到结论；
（2）分别求出两个半平面的法向量，再代入向量的夹角计算公式即可得到结论．

解答：解：（1）证明：∵AA₁⊥底面ABC，∴AA₁⊥AC，AA₁⊥AB．
又∵AB⊥AC，
∴以A为原点，AC，AB，AA₁所在的直线分别为x轴，y轴，z轴建立直角坐标系．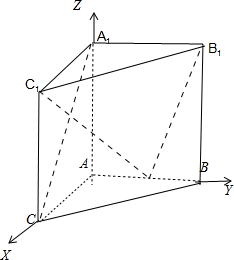
又∵V ABC-A 1B 1C 1 =

1

2

AB×AC×AA₁=1，∴AB=2．（2分）
设AP=m，则P（0，m，0），而C₁（1，0，1），C（1，0，0），A₁（0，0，1），B₁（0，2，1）
∴

CA1

=（-1，0，1），

C1P

=（-1，m，-1），

B1C1

=（-1，2，0）
∴

CA1

•

C1P

=（-1）×（-1）+0×m+1×（-1）=0，
∴CA₁⊥C₁P．（6分）
（2）设平面C₁PB₁的一个法向量

n

=（x，y，z），

n • B1C1 =0  n • C1P =0

⇒

-x+2y=0 -x+my-z=0

令y=1，则

n

=（2，1，m-2），（9分）
而平面A₁B₁P的一个法向量

AC

=（1，0，0），
依题意可知cos

π

6

=

|n• AC |

|n|| AC |

=

3

2

，
∴m=2+

3

3

（舍去）或m=2-

3

3

．
∴当AP=2-

3

3

时，二面角C₁-PB₁-A₁的大小为

π

6

．（12分）

点评：本题主要考查用空间向量求平面间的夹角以及用向量语言表述线线的垂直、平行关系．是对向量知识在立体几何中应用的综合考察．