题目内容

20．若双曲线与椭圆4x2+y2=64有公共的焦点，它们的离心率互为倒数，则双曲线的方程是（　　）
A．3y2-x2=36B．x2-3y2=36C．3x2-y2=36D．y2-3x2=36

分析 求出椭圆焦点为（0，±4$\sqrt{3}$），离心率为$\frac{\sqrt{3}}{2}$，利用双曲线与椭圆4x2+y2=64有公共的焦点，它们的离心率互为倒数，即可求双曲线方程．

解答 解：椭圆4x2+y2=64，即$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{64}$=1，
焦点为（0，±4$\sqrt{3}$），离心率为$\frac{\sqrt{3}}{2}$，
所以双曲线的焦点在y轴上，c=4$\sqrt{3}$，e=$\frac{2}{\sqrt{3}}$，
所以a=6，b=2$\sqrt{3}$，
所以双曲线方程为$\frac{{y}^{2}}{36}-\frac{{x}^{2}}{12}$=1，即y2-3x2=36，
故选：D．

点评 本题考查椭圆、双曲线方程与性质，考查学生的计算能力，属于中档题．

练习册系列答案
相关题目
10．$已知\overrightarrow a=（sinθ，\frac{1}{3}），\overrightarrow b=（cosθ，-1），θ∈R$
（1）若$\overrightarrow a$∥$\overrightarrow b$，求tanθ的值；      
（2）若$\overrightarrow a⊥\overrightarrow b$，求sin2θ的值．
11．若函数$f（x）=lgsin（{ωx+\frac{π}{6}}）（{ω＞0}）$的最小正周期为π，则f（x）在[0，π]上的递减区间为[$\frac{π}{6}$，$\frac{5π}{12}$）．
8．有一段长为11米的木棍，现要折成两段，两段都不小于3米的概率有多大？
15．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$⊥（$\overrightarrow{a}$-$\overrightarrow{b}$），且|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=2$\sqrt{3}$，则$\overrightarrow{a}$与$\overrightarrow{b}$ 的夹角为$\frac{π}{6}$．
5．设集合A={x|$\frac{2x-1}{x-2}$≤0}，B={x||x|＜1}，则A∪B=（　　）
A．[-$\frac{1}{2}$，1）B．（-1，1）∪（1，2）C．（-1，2）D．[-$\frac{1}{2}$，2）
12．程序框图如图，若输入S=1，k=1，则输出的S为26．
9．函数f（x）=cos（x+φ）（0≤φ≤π）的定义域为R，若f（x）为奇函数，则φ=（　　）
A．0B．$\frac{π}{4}$C．$\frac{π}{2}$D．π
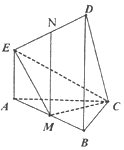10．如图所示的多面体中，EA⊥平面ABC，DB⊥平面ABC，AC⊥BC，且AC=BC=BD=2AE=2，M，N分别为AB，DE的中点．
（Ⅰ）求证：MN∥平面BCD；
（Ⅱ）求平面EMC与平面BCD所成的锐二面角的余弦值；
（Ⅲ）在线段CD上是否存在点F，使直线MF与平面EMC所成角为$\frac{π}{6}$，若存在，求出CF的长，若不存在说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网