题目内容
平面向量的集合A到A的映射f(
)=
-(
•
)•
,其中
为常向量,若f满足f(
)•f(
)=
•
对任意
,
∈A成立,则
的坐标可以是( )
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
分析:令
=
,可得f(
)•f(
)=[
-(
•
)•
]2=
2-2(
•
)2+[(
•
)
]2=
2,变形可解得|
|=0,或|
|=
,验证选项可得.
| y |
| x |
| x |
| x |
| x |
| x |
| a |
| a |
| x |
| x |
| a |
| x |
| a |
| a |
| x |
| a |
| a |
| 2 |
解答:解:令
=
,代入已知可得f(
)•f(
)=
•
,
又f(
)=
-(
•
)•
,
∴f(
)•f(
)=[
-(
•
)•
]2=
2-2(
•
)2+[(
•
)
]2=
2,
变形可得-2(
•
)2+[(
•
)
]2=0,即(
•
)2(-2+
2)=0
∴
=
,或
2=2,即|
|=0,或|
|=
验证选项可得B符合题意,
故选B
| y |
| x |
| x |
| x |
| x |
| x |
又f(
| x |
| x |
| x |
| a |
| a |
∴f(
| x |
| x |
| x |
| x |
| a |
| a |
| x |
| x |
| a |
| x |
| a |
| a |
| x |
变形可得-2(
| x |
| a |
| x |
| a |
| a |
| x |
| a |
| a |
∴
| a |
| 0 |
| a |
| a |
| a |
| 2 |
验证选项可得B符合题意,
故选B
点评:本题考查平面向量数量积的运算,涉及映射的知识和抽象函数的赋值法,属中档题.

练习册系列答案
相关题目
平面向量的集合A到A的映射f由f(
)=
-2(
•
)
确定,其中
为常向量.若映射f满足f(
) •f(
) =
•
对
,
∈A恒成立,则
的坐标不可能是( )
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
| A、(0,0) | ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-
|
 )=
)=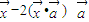 确定,其中
确定,其中 为常向量.若映射f满足
为常向量.若映射f满足 对
对 恒成立,则
恒成立,则 的坐标不可能是( )
的坐标不可能是( ) ,
, )
) ,
, )
) ,
, )
) )=
)=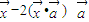 确定,其中
确定,其中 为常向量.若映射f满足
为常向量.若映射f满足 对
对 恒成立,则
恒成立,则 的坐标不可能是( )
的坐标不可能是( ) ,
, )
) ,
, )
) ,
, )
)