题目内容
平面向量的集合A到A的映射f由f(
)=
-2(
•
)
确定,其中
为常向量.若映射f满足f(
) •f(
) =
•
对
,
∈A恒成立,则
的坐标不可能是( )
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
| A、(0,0) | ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-
|
分析:通过赋值列出关于向量的方程,通过向量的运算法则化简方程,得到
满足的条件.
| a |
解答:解:令
=
,则f(
)•f(
)=
•
=[
-2(
•
)
]2=
2-4(
•
)2+4 [(
•
)
]2
即-4(
•
)2+4[(
•
)
]2=0,
∴(
•
)2(
2-1)=0
∴
=0或|
|=1
故选项为B.
| y |
| x |
| x |
| x |
| x |
| x |
| x |
| x |
| a |
| a |
| x |
| x |
| a |
| x |
| a |
| a |
即-4(
| x |
| a |
| x |
| a |
| a |
∴(
| x |
| a |
| a |
∴
| a |
| a |
故选项为B.
点评:本题考查向量的运算法则及向量的运算律.

练习册系列答案
相关题目
 )=
)=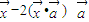 确定,其中
确定,其中 为常向量.若映射f满足
为常向量.若映射f满足 对
对 恒成立,则
恒成立,则 的坐标不可能是( )
的坐标不可能是( ) ,
, )
) ,
, )
) ,
, )
) )=
)=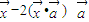 确定,其中
确定,其中 为常向量.若映射f满足
为常向量.若映射f满足 对
对 恒成立,则
恒成立,则 的坐标不可能是( )
的坐标不可能是( ) ,
, )
) ,
, )
) ,
, )
)