题目内容
13.已知集合A={x||x|≤1},B={x|x2-ax≤0},若A∩B=B.则实数a的取值范围是[-1,1].分析 化简A=[-1,1],结合B⊆A,分类讨论以确定集合B,从而解得.
解答 解:A={x||x|≤1}=[-1,1],
∵A∩B=B,
∴B⊆A,
①当a<0时,B={x|x2-ax≤0}=[a,0],
∴a∈[-1,0),
②当a=0时,B={x|x2-ax≤0}={0},
∴a=0,
③当a>0时,B={x|x2-ax≤0}=[0,a],
∴a∈(0,1],
综上所述,a∈[-1,1],
故答案为:[-1,1].
点评 本题考查了集合的化简与运算,同时考查了集合包含关系的应用及分类讨论的思想应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在△ABC中,若a2-b2=$\sqrt{3}$bc,且$\frac{sin(A+B)}{sinB}$=2$\sqrt{3}$,则角A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
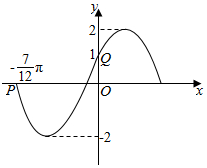 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示.试确定该函数的解析式.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示.试确定该函数的解析式.