题目内容
已知f（x）是周期为8的奇函数，当x∈[0，2]时，f（x）=2x，则f（-9）等于
- A.-4
- B.-2
- C.2
- D.4
B
分析：由f（x）是周期为8的奇函数，知f（-9）=f（-1）=-f（1），再由当x∈[0，2]时，f（x）=2x，能求出结果．
解答：∵f（x）是周期为8的奇函数，
当x∈[0，2]时，f（x）=2x，
∴f（-9）=f（-1）=-f（1）=-2．
故选B．
点评：本题考查函数性质的应用，解题时要认真审题，注意函数的奇偶性、周期性的灵活运用．
分析：由f（x）是周期为8的奇函数，知f（-9）=f（-1）=-f（1），再由当x∈[0，2]时，f（x）=2x，能求出结果．
解答：∵f（x）是周期为8的奇函数，
当x∈[0，2]时，f（x）=2x，
∴f（-9）=f（-1）=-f（1）=-2．
故选B．
点评：本题考查函数性质的应用，解题时要认真审题，注意函数的奇偶性、周期性的灵活运用．
练习册系列答案
轻松暑假总复习系列答案
相关题目
已知f（x）是周期为2的奇函数，当0＜x＜1时，f（x）=lgx．设a=f(
)，b=f(
)，c=f(
)，则（ ）
| 6 |
| 5 |
| 3 |
| 2 |
| 5 |
| 2 |
| A、a＜b＜c |
| B、b＜a＜c |
| C、c＜b＜a |
| D、c＜a＜b |
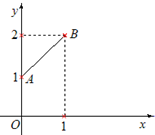已知f（x）是周期为2的偶函数．当0≤x≤1时，f（x）的图象是如图中的线段AB，那么