题目内容
设
＜α＜
，sin(α-
)=
，则
的值为
．
| π |
| 3 |
| 3π |
| 4 |
| π |
| 4 |
| 3 |
| 5 |
| sinα-cos2α+1 |
| tanα |
5
| ||
| 50 |
5
| ||
| 50 |
分析：首先根据角的范围以及同角三角函数的基本关系求出cos（α-
）、sinα、cosα的值，然后利用二倍角公式化简所求的式子，并将相应的值代入即可．
| π |
| 4 |
解答：解：∵
＜α＜
，
∴
＜α-
＜
∵sin(α-
)=
∴cos（α-
）=
=
．
∴sinα=sin[（α-
）+
]
=sin（α-
）cos
+cos（α-
）sin
=
×
+
×
=
∴cosα=
=
tanα=
=7
∴
=
=
=cosα（1+2sinα）
=
（1+2×
）
=
．
故答案为：
．
| π |
| 3 |
| 3π |
| 4 |
∴
| π |
| 12 |
| π |
| 4 |
| π |
| 2 |
∵sin(α-
| π |
| 4 |
| 3 |
| 5 |
∴cos（α-
| π |
| 4 |
1-sin2(α-
|
| 4 |
| 5 |
∴sinα=sin[（α-
| π |
| 4 |
| π |
| 4 |
=sin（α-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
=
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| ||
| 2 |
7
| ||
| 10 |
∴cosα=
| 1-sin2α |
| ||
| 10 |
tanα=
| sinα |
| cosα |
∴
| sinα-cos2α+1 |
| tanα |
=
| sinα+2sin2α |
| tanα |
=
| sinα(1+2sinα) | ||
|
=cosα（1+2sinα）
=
| ||
| 10 |
7
| ||
| 10 |
=
5
| ||
| 50 |
故答案为：
5
| ||
| 50 |
点评：本题主要考查同角三角函数的基本关系、二倍角公式等，求出sinα是解题的关键，属于中档题．
练习册系列答案
相关题目
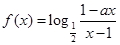为奇函数，
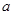为常数．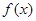
在区间（1，＋∞）内的单调性，并证明你的判断正确；
的值，不等式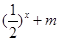
恒成立，求实数
的取值范围．
B,x∈A,求：
等于( ).