题目内容

15．已知平面α∩β=l，直线a?α，a∩l=A，直线b?β，b∩l=B，A与B不重合，求证：直线a与b是异面直线．

分析 证明直线a与b是异面直线，比较困难，考虑使用反证法．

解答 证明：用反证法：
若a与b不是异面直线，则a∥b或a与b相交
（1）若a∥b，则a∥β，∵平面α∩β=l，直线a?α，∴a∥l，这与a∩l=A矛盾；
（2）若a与b相交于B，则A与B重合，这与A与B不重合矛盾
∴直线a与b是异面直线．

点评 本题考查异面直线的判定，考查学生发现问题解决问题的能力，是中档题．

练习册系列答案
相关题目
5．设$\overrightarrow{a}$=（-2，3），$\overrightarrow{b}$=（-8，5），则5$\overrightarrow{a}$-3$\overrightarrow{b}$=（14，0）．
6．命题p：?a∈（-∞，-$\frac{1}{4}$]，使得函数f（x）=|2x+$\frac{a}{{2}^{x}}$|在[-$\frac{1}{2}$，3]上单调递增；命题q：?a∈[2，+∞），直线2x+y=0与双曲线$\frac{{y}^{2}}{{a}^{2}}$-x2=1（a＞0）相交．则下列命题中正确的是（　　）
A．￢pB．p∧qC．（￢p）∨qD．p∧（￢q）
3．在数列{an}中，an+1=an+t（n∈N*），其前n项和Sn=A•n2+B•n+c，则实数c为（　　）
A．-1B．0C．1D．2
10．求由直线x=1，x=3，y=0和曲线y=3x2所围成的图形的面积．
20．在△ABC中，角A，B，C所对的边分别为a，b，c，且$\frac{tanB}{tanA+tanB}$=$\frac{b}{2c}$
（I）求角A；
（Ⅱ）若$\overrightarrow{a}$=（0，-1），$\overrightarrow{b}$=（cosB，2cos2$\frac{C}{2}$），求|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围．
7．当x∈[-2，0）时，不等式ax3-x2+4x+3≥0恒成立，则实数a的取值范围是a≤-2．
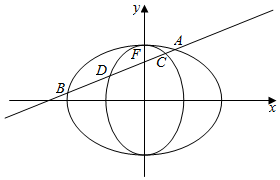6．如图的椭圆C1，C2的离心率相等，中心均为坐标原点，焦点分别在x轴和y轴上，且两椭圆都过点（0，$\sqrt{2}$），设点F是椭圆C2的上焦点，过点F的动直线l交椭圆C1于A，B两点，交椭圆C2于C，D两点，当直线l经过椭圆C1的左焦点时，$\frac{|AB|}{|CD|}$=$\frac{5\sqrt{2}}{4}$．
（1）求椭圆C1，C2的标准方程；
（2）平面内是否存在与点F不同的定点P，使得∠APC=∠BPD恒成立？若存在，求出定点P的坐标，若不存在，请说明理由．
7．sin80°cos20°-cos80°sin20°的值为$\frac{\sqrt{3}}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网