题目内容
函数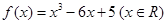 ,若关于
,若关于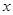 的方程
的方程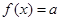 有三个不同实根,则
有三个不同实根,则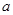 的取值范围是
的取值范围是
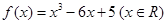 ,若关于
,若关于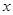 的方程
的方程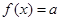 有三个不同实根,则
有三个不同实根,则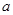 的取值范围是
的取值范围是 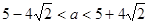
试题分析:因为,
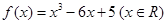 ,所以f′(x)=3(x2-2),
,所以f′(x)=3(x2-2),令f′(x)=0,得x1=-
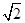 ,x2=
,x2=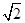 ,
,∴当 x<-
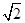 或x>
或x>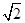 时,f′(x)>0,
时,f′(x)>0,当-
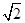 <x<
<x<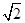 时,f′(x)<0,
时,f′(x)<0,∴f(x)的单调递增区间是 (-∞,-
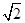 )和(
)和(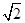 ,+∞),单调递减区间是 (-
,+∞),单调递减区间是 (-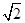 ,
,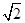 ),
),当 x=-
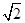 ,f(x)有极大值5+4
,f(x)有极大值5+4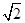 ;当 x=
;当 x=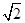 ,f(x)有极小值5-4
,f(x)有极小值5-4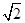 ,
,由上分析可知y=f(x)图象的大致形状及走向,
∴当
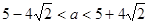 时,直线y=a与y=f(x)的图象有3个不同交点,
时,直线y=a与y=f(x)的图象有3个不同交点,即方程f(x)=α有三解.
故答案为
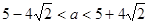 。
。点评:中档题,本题通过利用导数研究函数的单调性、图象、极值等,明确了函数的图象大致形态,从而确定得到参数a的取值范围。很好地体现了数形结合、转化与化归的思想方法,具有较强的代表性。

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
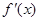 >
>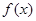 成立,则称函数
成立,则称函数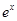 lnx是J函数时,求m的取值范围;
lnx是J函数时,求m的取值范围;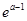 g(1)的大小;
g(1)的大小;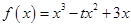 ,若对于任意的
,若对于任意的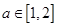 ,
,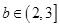 ,函数
,函数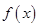 在区间
在区间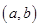 上单调递减,则实数
上单调递减,则实数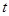 的取值范围是( )
的取值范围是( )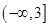
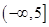
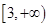

 在
在 是增函数,则a的取值范围是( )
是增函数,则a的取值范围是( )



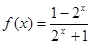 ,请用定义证明
,请用定义证明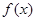 在
在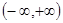
 上为减函数.
上为减函数.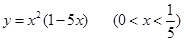 的最大值是
的最大值是 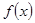 是奇函数,且在区间
是奇函数,且在区间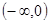 上是单调增函数,又
上是单调增函数,又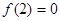 ,则
,则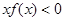 的解集为 .
的解集为 .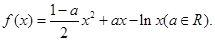
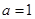 时,求函数
时,求函数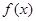 的极值;
的极值;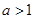 时,讨论函数
时,讨论函数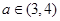 及任意
及任意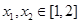 ,恒有
,恒有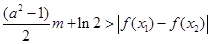 成立,求实数
成立,求实数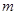 的取值范围.
的取值范围.