题目内容
抛物线C1：y＝
x2(p>0)的焦点与双曲线C2：
－y2＝1的右焦点的连线交C1于第一象限的点M，若C1在点M处的切线平行于C2的一条渐近线，则p＝( )
A.
B.
C.
D.
D
[解析] 由已知抛物线x2＝2py(p>0)的焦点为A(0，
)，双曲线－y2＝1的右焦点为B(2,0)，渐近线方程为y＝±
x.
设M(x0，y0)，则y0＝
，
由kMA＝kAB得
(1)
由y＝
知，y′＝
，则y′|x＝x0＝
＝，
代入(1)式中消去x0并解之得p＝.
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
D．5
过点A(2,1)和B(5,2)，记an＝3f(n)(n∈N*)．
，Tn＝b1＋b2＋…＋bn，若Tn＜m(m∈Z)对n
∈N*恒成立，求m的最小值．
x＋φ)(0<φ<π)，若f(x)＋f ′(x)为奇函数，则φ＝________.
.
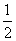ax2－2x存在单调递减区间，则实数a的取值范围是________．