题目内容
已知α,β∈(0,π),且tanα=2,cosβ=- .
.
(1)求cos2α的值;
(2)求2α-β的值.
 .
.(1)求cos2α的值;
(2)求2α-β的值.
(1)- (2)-
(2)-
 (2)-
(2)-
解:(1)cos2α=cos2α-sin2α= =
= =
= =-
=- .
.
(2)因为α∈(0,π),且tanα=2,所以α∈(0, ).
).
又cos2α=- <0,故2α∈(
<0,故2α∈( ,π),sin2α=
,π),sin2α= .
.
由cosβ=- ,β∈(0,π),
,β∈(0,π),
得sinβ= ,β∈(
,β∈( ,π).
,π).
所以sin(2α-β)=sin2αcosβ-cos2αsinβ= ×(-
×(- )-(-
)-(- )×
)× =-
=- .
.
又2α-β∈(- ,
, ),所以2α-β=-
),所以2α-β=- .
.
 =
= =
= =-
=- .
.(2)因为α∈(0,π),且tanα=2,所以α∈(0,
 ).
).又cos2α=-
 <0,故2α∈(
<0,故2α∈( ,π),sin2α=
,π),sin2α= .
.由cosβ=-
 ,β∈(0,π),
,β∈(0,π),得sinβ=
 ,β∈(
,β∈( ,π).
,π).所以sin(2α-β)=sin2αcosβ-cos2αsinβ=
 ×(-
×(- )-(-
)-(- )×
)× =-
=- .
.又2α-β∈(-
 ,
, ),所以2α-β=-
),所以2α-β=- .
.
练习册系列答案
相关题目
 ,求
,求 的值.
的值. ,tan
,tan =
= ,则cosβ的值为________.
,则cosβ的值为________. +2α)=sin(
+2α)=sin( +α),则tan2α的值为( )
+α),则tan2α的值为( )



 ,sin(
,sin( ,求
,求 的值.
的值. 中,a,b,c分别是角A、B、C所对的边,若
中,a,b,c分别是角A、B、C所对的边,若
 ,若则
,若则 的最大值为 .
的最大值为 . =( )
=( )


 ,
, ,则
,则 ( )
( )

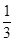
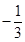
 ,
, ,那么
,那么 的值为________ .
的值为________ .