题目内容
如图,正方体 的棱长为
的棱长为 ,
, 、
、 分别是
分别是 、
、 的中点.
的中点.

⑴求多面体 的体积;
的体积;
⑵求 与平面
与平面 所成角的余弦值.
所成角的余弦值.
 的棱长为
的棱长为 ,
, 、
、 分别是
分别是 、
、 的中点.
的中点.
⑴求多面体
 的体积;
的体积;⑵求
 与平面
与平面 所成角的余弦值.
所成角的余弦值. (1)
(2)

(2)

试题分析:⑴
 ……1分,
……1分, ……2分,
……2分, ……3分,所以,多面体
……3分,所以,多面体 的体积
的体积 ……4分
……4分⑵以
 为原点,
为原点, 、
、 、
、 分别为
分别为 轴、
轴、 轴、
轴、 轴建立空间直角坐标系……5分,则
轴建立空间直角坐标系……5分,则 ,
, ,
, ,
, ……6分,设平面
……6分,设平面 的一个法向量为
的一个法向量为 ,则
,则 ……8分,即
……8分,即
9分,取
 ,则
,则 ……10分,
……10分, 11分,
11分, 12分,
12分, 与平面
与平面 所成角的余弦值
所成角的余弦值 13分。
13分。点评:主要是考查了线面角的求解以及锥体体积的求解,属于中档题。

练习册系列答案
相关题目
 ,E为DC的中点,将它沿AE折成直二面角D-AE-B.
,E为DC的中点,将它沿AE折成直二面角D-AE-B.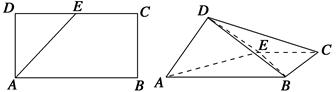
 的底面
的底面 是正方形,
是正方形, 平面
平面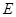 为
为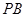 上的点,且
上的点,且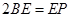 .
.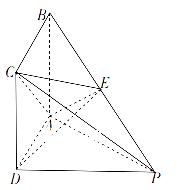
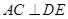 ;
; ,求二面角
,求二面角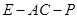 的余弦值.
的余弦值.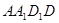 与矩形
与矩形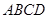 所在平面互相垂直,
所在平面互相垂直,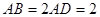 ,点
,点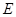 为
为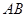 的中点.
的中点.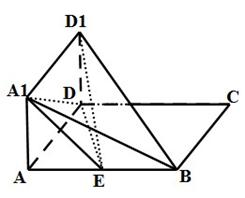
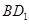 ∥平面
∥平面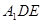 ;
;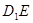
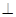
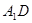 ;
;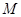 ,使二面角
,使二面角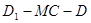 的大小为
的大小为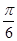 ?若存在,求出
?若存在,求出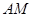 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. 中,
中, ,
, ,
, ,点
,点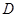 是
是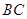 的中点.
的中点.
 与
与 所成角的余弦值;
所成角的余弦值; 与平面
与平面 所成二面角的正弦值.
所成二面角的正弦值.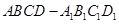 中,底面
中,底面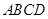 为平行四边形,且
为平行四边形,且 ,
,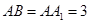 ,
,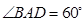 ,
,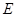 为
为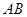 的中点.
的中点.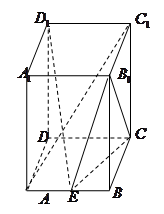
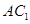 ∥平面
∥平面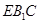 ;
;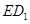 与平面
与平面
 的底面为直角梯形,
的底面为直角梯形, ,
,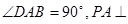 底面
底面 ,且
,且 ,
, ,
, 是
是 的中点。
的中点。 面
面 ;
; 与
与 与面
与面 所成二面角的余弦值.
所成二面角的余弦值.