题目内容
设
=(cosα,sinα),
=(cosβ,sinβ),则|3
-4
|的最大值是( )
| a |
| b |
| a |
| b |
分析:利用两个向量的加减法的法则求出向量 3
-4
的坐标,要求的式子可化为
,故当cos(α-β)
=-1 时,要求的式子有最大值为7.
| a |
| b |
| 25-24cos(α-β) |
=-1 时,要求的式子有最大值为7.
解答:解:由题意可得 3
-4
=(3cosα-4cosβ,3sinα-4sinβ),
∴|3
-4
|=
=
=
,
故当cos(α-β)=-1 时,要求的式子有最大值为7,
故选C.
| a |
| b |
∴|3
| a |
| b |
| (3cosα -4cosβ)2+( 3sinα - 4sinβ)2 |
| 9+16-24cos(α-β) |
| 25-24cos(α-β) |
故当cos(α-β)=-1 时,要求的式子有最大值为7,
故选C.
点评:本题考查两个向量的加减法的法则,两个向量坐标形式的运算,求向量的模的方法,求三角函数的最值,把要求的式子
化为
,是解题的关键.
化为
| 25-24cos(α-β) |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
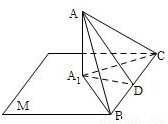
 已知△ABC的一边BC在平面M内,从A作平面M的垂线,垂足是A1,设△ABC的面积是S,它与平面M组成的二面角等于α(0°<α<90°),求证:△A1BC的面积=S•cosα.
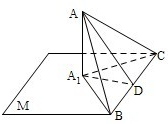
已知△ABC的一边BC在平面M内,从A作平面M的垂线,垂足是A1,设△ABC的面积是S,它与平面M组成的二面角等于α(0°<α<90°),求证:△A1BC的面积=S•cosα.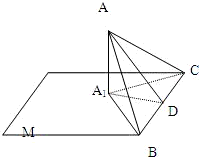 已知△ABC的一边BC在平面M内,从A作平面M的垂线,垂足是A1,设△ABC的面积是S,它与平面M组成的二面角等于α(0°<α<90°),求证:△A1BC的面积=S•cosα.
已知△ABC的一边BC在平面M内,从A作平面M的垂线,垂足是A1,设△ABC的面积是S,它与平面M组成的二面角等于α(0°<α<90°),求证:△A1BC的面积=S•cosα.