题目内容
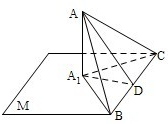 已知△ABC的一边BC在平面M内,从A作平面M的垂线,垂足是A1,设△ABC的面积是S,它与平面M组成的二面角等于α(0°<α<90°),求证:△A1BC的面积=S•cosα.
已知△ABC的一边BC在平面M内,从A作平面M的垂线,垂足是A1,设△ABC的面积是S,它与平面M组成的二面角等于α(0°<α<90°),求证:△A1BC的面积=S•cosα.
分析:由题意及所给的图形,利用三垂线定理及二面角平面角的概念和三角形的面积公式即可得证.
解答:证明:在△ABC中,作AD⊥BC,
垂足为D,连接A1D,A1B,A1C,
因AD⊥BC,由三垂线定理可得
A1D⊥BC,
所以∠ADA1为平面ABC与平面M所构成的二面角的平面角,
∴∠ADA1=α
在△AA1D中,A1D=AD•cosα
∴△A1BC的面积=
•A1D•BC=
•AD•BC•cosα=△ABC的面积•cosα=S•cosα.
垂足为D,连接A1D,A1B,A1C,
因AD⊥BC,由三垂线定理可得
A1D⊥BC,
所以∠ADA1为平面ABC与平面M所构成的二面角的平面角,
∴∠ADA1=α
在△AA1D中,A1D=AD•cosα
∴△A1BC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题重点考查了利用三垂线定理,借助二面角平面角的概念及三角形的面积公式得到以后常用的利用投影面积法求解二面角的大小这一常用的方法.

练习册系列答案
相关题目
 有两解 B.
有两解 B.  有一解
有一解 无解 D.
无解 D.  有一解
有一解