题目内容
14.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=ex+x2+1,则函数h(x)=2f(x)-g(x)在点(0,h(0))处的切线方程是x-y+4=0.分析 由题意可得f(-x)=f(x),g(-x)=-g(x),将已知条件中的方程的x换为-x,解方程可得f(x),g(x)的解析式,求得h(x)的解析式和导数,可得切线的斜率和切点,运用点斜式方程可得所求切线的方程.
解答 解:f(x),g(x)分别是定义在R上的偶函数和奇函数,
可得f(-x)=f(x),g(-x)=-g(x),
由f(x)-g(x)=ex+x2+1,
可得f(-x)-g(-x)=e-x+x2+1,
即为f(x)+g(x)=e-x+x2+1,
解得$f(x)=\frac{{{e^x}+{e^{-x}}+2{x^2}+2}}{2}$,$g(x)=\frac{{{e^{-x}}-{e^x}}}{2}$,
即有h(x)=2f(x)-g(x)=${e^x}+{e^{-x}}+2{x^2}+2-\frac{{{e^{-x}}-{e^x}}}{2}$
=$\frac{3}{2}{e^x}+\frac{1}{2}{e^{-x}}+2{x^2}+2$,
可得导数为$h'(x)=\frac{3}{2}{e^x}+\frac{1}{2}{e^{-x}}•(-1)+4x$,
即有在点(0,h(0))处的切线斜率为$h'(0)=\frac{3}{2}-\frac{1}{2}=1$,
切点为(0,4),
则所求切线方程是x-y+4=0.
故答案为:x-y+4=0.
点评 本题主要考查导数的运用:求切线的方程,注意运用导数的几何意义,同时考查函数的解析式的求法,注意运用奇偶函数的定义,考查化简整理的运算能力,属于中档题.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
19.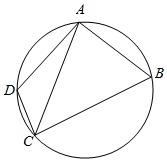 如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
 如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
6.已知实数x,y满足xy-3=x+y,且x>1,则y(x+8)的最小值是( )
| A. | 33 | B. | 26 | C. | 25 | D. | 21 |

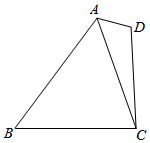 如图,在四边形ABCD中,AB=4,AC=2$\sqrt{3}$,cos∠ACB=$\frac{1}{3}$,∠D=2∠B.
如图,在四边形ABCD中,AB=4,AC=2$\sqrt{3}$,cos∠ACB=$\frac{1}{3}$,∠D=2∠B.