题目内容
 (2012•福建)如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2012•福建)如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )分析:根据题意,易得正方形OABC的面积,观察图形可得,阴影部分由函数y=x与y=
围成,由定积分公式,计算可得阴影部分的面积,进而由几何概型公式计算可得答案.
| x |
解答:解:根据题意,正方形OABC的面积为1×1=1,
而阴影部分由函数y=x与y=
围成,其面积为∫01(
-x)dx=(
x
-
)|01=
,
则正方形OABC中任取一点P,点P取自阴影部分的概率为
=
;
故选C.
而阴影部分由函数y=x与y=
| x |
| x |
| 2 |
| 3 |
| 3 |
| 2 |
| x2 |
| 2 |
| 1 |
| 6 |
则正方形OABC中任取一点P,点P取自阴影部分的概率为
| ||
| 1 |
| 1 |
| 6 |
故选C.
点评:本题考查几何概型的计算,涉及定积分在求面积中的应用,关键是正确计算出阴影部分的面积.

练习册系列答案
相关题目
 (2012•福建)如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.
(2012•福建)如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.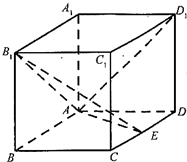 (2012•福建)如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.
(2012•福建)如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点. (2012•福建)如图,等边三角形OAB的边长为
(2012•福建)如图,等边三角形OAB的边长为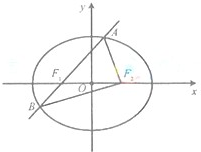 (2012•福建)如图,椭圆E:
(2012•福建)如图,椭圆E: