题目内容
定义函数fn(x)=(1+x)n-1,x>-2,x∈N*.(1)求证:fn(x)≥nx;
(2)是否存在区间[a,0](a<0),使函数h(x)=f3(x)-f2(x)在区间[a,0]上的值域为[ka,0]若存在,求出最小的k值及相应的区间[a,0],若不存在,说明理由.
【答案】分析:(1)令g(x)=fn(x)-nx=(1+x)n-1-nx,求出导函数,利用导数研究函数的增减性得到函数的最小值为g(0)=0,即可得证;
(2)h(x)=f3(x)-f2(x)=x(1+x)2,x∈[a,0](a<0),求导函数,分类讨论,确定函数的最值,利用函数h(x)=f3(x)-f2(x)在区间[a,0]上的值域为[ka,0],即可求得结论.
解答: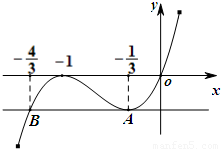 (1)证明:令g(x)=fn(x)-nx=(1+x)n-1-nx.
(1)证明:令g(x)=fn(x)-nx=(1+x)n-1-nx.
则g'(x)=n(x+1)n-1-n=n[(x+1)n-1-1],
∴当-2<x<0时,g'(x)<0;当x>0时g'(x)>0.
∴g(x)在(-2,0)上单调递减,在(0,+∞)上单调递增.
∴当x=0时,g(x)min=g(0)=0,即g(x)≥g(x)min=g(0)=0,
∴fn(x)≥nx;
(2)解:h(x)=f3(x)-f2(x)=x(1+x)2,x∈[a,0](a<0),
∴h'(x)=(1+x)2+2x(1+x)=(1+x)(1+3x),
令h'(x)=0,得x=-1或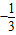
∵h(-1)=h(0)=0,h( )=h(
)=h(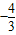 )=-
)=-
∴若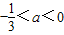 ,则函数在[a,0]上单调增,∴h(a)=ka,h(0)=0,∴a(1+a)2=ka,∴k=(1+a)2∈(
,则函数在[a,0]上单调增,∴h(a)=ka,h(0)=0,∴a(1+a)2=ka,∴k=(1+a)2∈(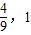 );
);
若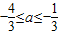 ,则h(
,则h(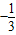 )=ka,h(0)=0,∴k=-
)=ka,h(0)=0,∴k=-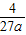 ∈
∈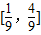 ;
;
若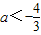 ,则h(a)=ka,h(0)=0,∴a(1+a)2=ka,∴k=(1+a)2∈(
,则h(a)=ka,h(0)=0,∴a(1+a)2=ka,∴k=(1+a)2∈( ,+∞)
,+∞)
综上知,k∈[ ,+∞)
,+∞)
∴最小的k值为 ,相应的区间为[
,相应的区间为[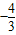 ,0]
,0]
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查分类讨论的数学思想,综合性强.
(2)h(x)=f3(x)-f2(x)=x(1+x)2,x∈[a,0](a<0),求导函数,分类讨论,确定函数的最值,利用函数h(x)=f3(x)-f2(x)在区间[a,0]上的值域为[ka,0],即可求得结论.
解答:
 (1)证明:令g(x)=fn(x)-nx=(1+x)n-1-nx.
(1)证明:令g(x)=fn(x)-nx=(1+x)n-1-nx.则g'(x)=n(x+1)n-1-n=n[(x+1)n-1-1],
∴当-2<x<0时,g'(x)<0;当x>0时g'(x)>0.
∴g(x)在(-2,0)上单调递减,在(0,+∞)上单调递增.
∴当x=0时,g(x)min=g(0)=0,即g(x)≥g(x)min=g(0)=0,
∴fn(x)≥nx;
(2)解:h(x)=f3(x)-f2(x)=x(1+x)2,x∈[a,0](a<0),
∴h'(x)=(1+x)2+2x(1+x)=(1+x)(1+3x),
令h'(x)=0,得x=-1或
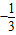
∵h(-1)=h(0)=0,h(
 )=h(
)=h(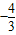 )=-
)=-
∴若
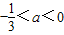 ,则函数在[a,0]上单调增,∴h(a)=ka,h(0)=0,∴a(1+a)2=ka,∴k=(1+a)2∈(
,则函数在[a,0]上单调增,∴h(a)=ka,h(0)=0,∴a(1+a)2=ka,∴k=(1+a)2∈(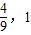 );
);若
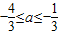 ,则h(
,则h(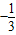 )=ka,h(0)=0,∴k=-
)=ka,h(0)=0,∴k=-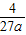 ∈
∈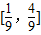 ;
;若
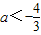 ,则h(a)=ka,h(0)=0,∴a(1+a)2=ka,∴k=(1+a)2∈(
,则h(a)=ka,h(0)=0,∴a(1+a)2=ka,∴k=(1+a)2∈( ,+∞)
,+∞)综上知,k∈[
 ,+∞)
,+∞)∴最小的k值为
 ,相应的区间为[
,相应的区间为[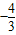 ,0]
,0]点评:本题考查导数知识的运用,考查函数的单调性与最值,考查分类讨论的数学思想,综合性强.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目