题目内容
4.若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是②③(填空写所有正确选项的序号)①y=$\left\{\begin{array}{l}{{x}^{3},x>0}\\{-x-1,x<0}\end{array}\right.$;②y=$\left\{\begin{array}{l}{\frac{1}{2}x-1,x>0}\\{-ln|x|,x<0}\end{array}\right.$;③y=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{-{x}^{2}-4x,x<0}\end{array}\right.$;④y=$\left\{\begin{array}{l}{3x+\frac{1}{2},x>0}\\{{e}^{-x},x<0}\end{array}\right.$.
分析 根据“伙伴点组”的定义可知,只需要利用图象,作出函数f(x)则x<0时关于原点对称的图象,利用对称图象在x>0两个图象的交点个数,即为“伙伴点组”的个数.根据条件进行判断即可.
解答 解:①函数y=-x-1,(x<0)关于原点对称的函数为-y=x-1,即y=-x+1,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数只有一个,所以函数f(x)的“伙伴点组”有1个,不满足条件.
②函数y=-ln|x|(x<0)关于原点对称的函数为-y=-ln|-x|,即y=ln|x|,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有2个,所以函数f(x)的“伙伴点组”有2个,满足条件.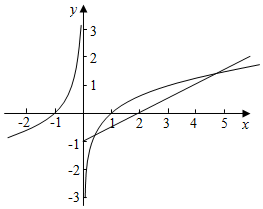
③函数y=-x2-4x,(x<0)关于原点对称的函数为-y=-x2+4x,即y=x2-4x,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有2个,所以函数f(x)的“伙伴点组”有2个,满足条件.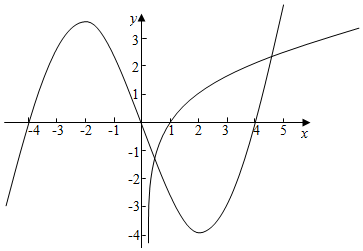
④函数y=e-x,(x<0)关于原点对称的函数为-y=ex,即y=-ex,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有0个,所以函数f(x)的“伙伴点组”有0个,不满足条件.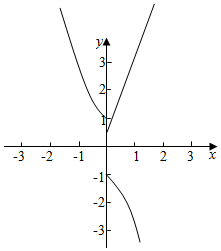 ,
,
故答案为:②③.
点评 本题主要考查新定义题目,读懂题意,利用数形结合的思想是解决本题的关键.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
12.执行如图的程序框图(N∈N*),那么输出的p是( )


| A. | $A_{N+3}^{N+3}$ | B. | $A_{N+2}^{N+2}$ | C. | $A_{N+1}^{N+1}$ | D. | $A_N^N$ |
19.f(x)是定义在(0,+∞)上单调函数,且对?x∈(0,+∞),都有f(f(x)-lnx)=e+1,则方程f(x)-f′(x)=e的实数解所在的区间是( )
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,e) | D. | (e,3) |
9.已知等差数列{an}的前n项和Sn满足S3=0,S5=5,则an=( )
| A. | 2-n | B. | n-2 | C. | -2-n | D. | n+2 |
16.如图所示的程序框图,输出结果中s=( )


| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |
13.设复数z满足$\frac{1-z}{1+z}$=i,则z的虚部为( )
| A. | -2 | B. | 0 | C. | -1 | D. | 1 |