题目内容
已知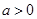 ,函数
,函数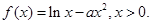 (
(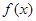 的图像连续不断)
的图像连续不断)
(Ⅰ)求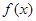 的单调区间;
的单调区间;
(Ⅱ)当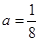 时,证明:存在
时,证明:存在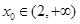 ,使
,使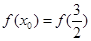 ;
;
(Ⅲ)若存在均属于区间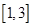 的
的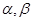 ,且
,且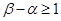 ,使
,使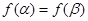 ,证明
,证明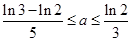 .
.
【答案】
(Ⅰ)解: , 令
, 令
 .
.
当x变化时, 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
+ |
0 |
- |
|
|
|
极大值 |
|
|
|
|
|
|
|
|
+ |
0 |
- |
|
|
|
极大值 |
|
|
|
|
|
|
|
|
+ |
0 |
- |
|
|
|
极大值 |
|

|
|
|
|
|
|
|
+ |
0 |
- |
|
|
|
极大值 |
|
所以, 的单调递增区间是
的单调递增区间是 的单调递减区间是
的单调递减区间是
(Ⅱ)证明:当
由(Ⅰ)知 在(0,2)内单调递增,在
在(0,2)内单调递增,在 内单调递减.令
内单调递减.令
由于 在(0,2)内单调递增,故
在(0,2)内单调递增,故 取
取
所以存在 即存在
即存在
(Ⅲ)证明:由 及(Ⅰ)的结论知
及(Ⅰ)的结论知 ,
,
从而 上的最小值为
上的最小值为 又由
又由 ,
, 知
知
故
从而
【解析】略

练习册系列答案
相关题目







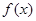 满足:①在x=1时有极值;②图像过点
满足:①在x=1时有极值;②图像过点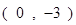 ,且在该点处的切线与直线
,且在该点处的切线与直线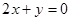 平行.
平行. 的值域;
的值域;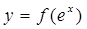 上任意两点的连线的斜率恒大于
上任意两点的连线的斜率恒大于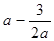 ,求
,求 的取值范围.
的取值范围. ,数列
,数列 的通项公式是
的通项公式是 ,前
,前 项和记作
项和记作 (
( 1,2,…),规定
1,2,…),规定 .函数
.函数 在
在 处和每个区间
处和每个区间 (
( 0,1,2,…)上有定义,且
0,1,2,…)上有定义,且 ,
, (
( 时,
时, (
( ,
, )与点
)与点 (
( ,
, )的线段上.
)的线段上. :
: (
( , 求
, 求 ;
; ,求
,求 的取值范围.
的取值范围.