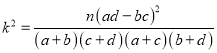题目内容
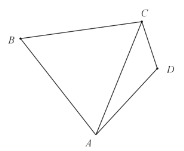
【题目】为了美化环境,某公园欲将一块空地规划建成休闲草坪,休闲草坪的形状为如图所示的四边形ABCD.其中AB=3百米,AD=![]() 百米,且△BCD是以D为直角顶点的等腰直角三角形.拟修建两条小路AC,BD(路的宽度忽略不计),设∠BAD=
百米,且△BCD是以D为直角顶点的等腰直角三角形.拟修建两条小路AC,BD(路的宽度忽略不计),设∠BAD=![]() ,
,![]() (
(![]() ,
,![]() ).
).
(1)当cos![]() =
=![]() 时,求小路AC的长度;
时,求小路AC的长度;
(2)当草坪ABCD的面积最大时,求此时小路BD的长度.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)在△ABD中,由余弦定理可求BD的值,利用同角三角函数基本关系式可求sinθ,根据正弦定理可求sin∠ADB![]() ,进而可求cos∠ADC的值,在△ACD中,利用余弦定理可求AC的值.
,进而可求cos∠ADC的值,在△ACD中,利用余弦定理可求AC的值.
(2)由(1)得:BD2=14﹣6![]() cosθ,根据三角形面积公式,三角函数恒等变换的应用可求.SABCD=7
cosθ,根据三角形面积公式,三角函数恒等变换的应用可求.SABCD=7![]() sin(θ﹣φ),结合题意当θ﹣φ
sin(θ﹣φ),结合题意当θ﹣φ![]() 时,四边形ABCD的面积最大,即θ=φ
时,四边形ABCD的面积最大,即θ=φ![]() ,此时cosφ
,此时cosφ![]() ,sinφ
,sinφ![]() ,从而可求BD的值.
,从而可求BD的值.
(1)在![]() 中,由
中,由![]() ,
,
得![]() ,又
,又![]() ,∴
,∴![]() .
.
∵![]() ∴
∴![]()
由![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∵![]() 是以
是以![]() 为直角顶点的等腰直角三角形 ∴
为直角顶点的等腰直角三角形 ∴![]() 且
且![]()
∴![]()
在![]()
![]()
![]() ,
,
解得:![]()
(2)由(1)得:![]() ,
,
![]()
![]()
![]() ,此时
,此时![]() ,
,![]() ,且
,且![]()
当![]() 时,四边形
时,四边形![]() 的面积最大,即
的面积最大,即![]() ,此时
,此时![]() ,
,![]()
∴![]() ,即
,即![]()
答:当![]() 时,小路
时,小路![]() 的长度为
的长度为![]() 百米;草坪
百米;草坪![]() 的面积最大时,小路
的面积最大时,小路![]() 的长度为
的长度为![]() 百米.
百米.

【题目】心理学家发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学,给所有同学几何和代数各一题,让各位同学自由选择一道题进行解答,统计情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男 同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)现从选择几何题的8名女生中任意抽取两人对他们的答题进行研究,记甲、乙两名女生被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
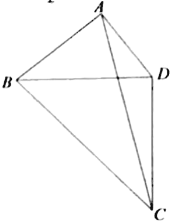
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |