Question

【题目】如图所示，在四棱锥P－ABCD中，PA⊥平面ABCD，AB＝4，BC＝3，AD＝5，∠DAB＝∠ABC＝90°，E是CD的中点．

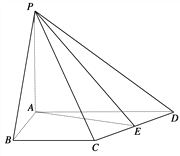
(1)证明：CD⊥平面PAE；

(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P－ABCD的体积．

Answer 1

【答案】（1）见解析；（2）.

【解析】试题分析：（Ⅰ）要证平面，由已知平面，已经有，因此在直角梯形中证明即可，通过计算得，而是中点，则有；（Ⅱ）PB与平面ABCD所成的角是，下面关键是作出PB与平面PAE所成的角，由（Ⅰ）作，分别与相交于，连接，则是PB与平面PAE所成的角，由这两个角相等，可得，同样在直角梯形中可计算出，也即四棱锥P-ABCD的高，体积可得．另外也可建立空间直角坐标系，通过空间向量法求得结论，第（Ⅱ）小题中关键是求点的坐标，注意这里直线与平面所成的角相等转化为直线与平面的法向量的夹角相等．

试题解析：解法1（Ⅰ如图（1）），连接AC，由AB=4，，

是的中点，所以

所以

而内的两条相交直线，所以CD⊥平面PAE．

（Ⅱ）过点Ｂ作

由（Ⅰ）CD⊥平面PAE知，ＢＧ⊥平面PAE．于是为直线ＰＢ与平面PAE

所成的角，且．

由知，为直线与平面所成的角．

由题意，知

因为所以

由所以四边形是平行四边形，故于是

在中，所以

于是

又梯形的面积为所以四棱锥的体积为

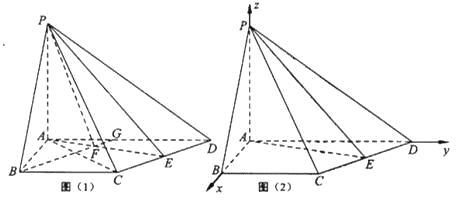
解法2：如图（2），以A为坐标原点，所在直线分别为建立空间直角坐标系．设则相关的各点坐标为：

（Ⅰ）易知因为

所以而是平面内的两条相交直线，所以

（Ⅱ）由题设和（Ⅰ）知，分别是，的法向量，而PB与

所成的角和PB与所成的角相等，所以

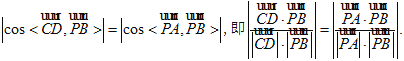
由（Ⅰ）知，由故

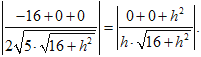
解得．

又梯形ABCD的面积为，所以四棱锥的体积为

．