题目内容

已知ab≠0，求a3+b3+ab-a2-b2=0的充要条件.?

思路分析：求充要条件就是求等价的条件，即化简

a3+b3+ab-a2-b2=0.

解：∵a3+b3+ab-a2-b2=0,

∴（a+b）（a2-ab+b2）-（a2+b2-ab）=0.?

即（a+b-1）（a2-ab+b2）=0.?

∵ab≠0,∴a2-ab+b2＞0.?

∴a+b-1=0.即a+b=1,??

由于以上每一步，都是等价转化.故当ab≠0时，a3+b3+ab-a2-b2=0的充要条件是a+b=1.

温馨提示

求充要条件时，需说明充分性和必要性两点，或寻求让结论成立的等价条件.

练习册系列答案
相关题目
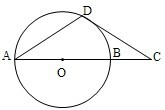精英家教网本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A：AB是圆O的直径，D为圆O上一点，过D作圆O的切线交AB延长线于点C，若DA=DC，求证：AB=2BC．
B：在平面直角坐标系xOy中，已知点A（0，0），B（-2，0），C（-2，1）．设k为非零实数，矩阵M=
k0
01
，N=
01
10
，点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1，△A1B1C1的面积是△ABC面积的2倍，求k的值．
C：在极坐标系中，已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切，求实数a的值．
D：设a、b是非负实数，求证：a3+b3≥
ab
(a2+b2)．
已知函数f（x）=x3+ax+b+（x∈R），且f（0）=1．
（1）若f（x）在R上单调递增，求实数a的取值范围；
（2）若y=f（x）在x=1处的切线与y轴交于点B，且A（1，f（1）），求d（a）=|AB|2在a∈[c，+∞]的最小值；
（3）若a=-
1
2
，Mn=f（1）+
1
2
f（2）+
1
3
f（3）+…+
1
n
f（n）-（1+
1
2
+
1
3
+…+
1
n
），an=
2n-1
6Mn
（n∈N*），Sn=a1+a3+…+an，求证：Sn＜
3
4
．
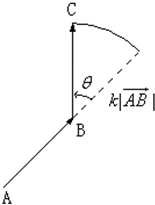精英家教网如图，
BC
的大小是
AB
大小的k倍，
BC
的方向由
AB
的方向逆时针旋转θ角得到，则我们称
AB
经过一次（θ，k）延伸得到
BC
． 已知
OA1
=(1，0)
（1）向量
OA1
经过2次(
π
2
，
1
2
)延伸，分别得到向量
A1A2
、
A2A3
，求
A1A2
、
A2A3
的坐标．
（2）向量
OA1
经过n-1次(
π
2
，
1
2
)延伸得到的最后一个向量
为
An-1An
，（n∈N*，n＞1），设点An（xn，yn），求An的极限位置A(
lim
n→∞
xn，
lim
n→∞
yn)
（3）向量
OA1
经过2次（θ，k）延伸得到向量
A1A2
、
A2A3
，其中k＞0，θ∈（0，π），若
OA1
、
A1A2
、
A2A3
恰能够构成一个三角形（即A3与O重合），求θ，k的值．
已知ab≠0，求a3+b3+ab-a2-b2=0的充要条件.?

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网